
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
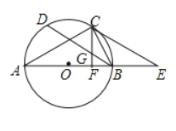
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)连接OC,首先根据题意得出![]() ,由此证明
,由此证明![]() ,然后利用平行线性质进一步得出
,然后利用平行线性质进一步得出![]() ,据此即可证明结论;
,据此即可证明结论;
(2)根据![]() 为直径可知
为直径可知![]() ,然后进一步利用
,然后进一步利用![]() 进行等量代换,从而得出
进行等量代换,从而得出![]() ,据此进一步即可证明结论;
,据此进一步即可证明结论;
(3)首先在Rt△BFG中利用勾股定理得出BF的长,然后根据平行线性质结合题意得出![]() ,再利用三角函数在Rt△CFE中求出EF的长,据此进一步计算即可得出答案.
,再利用三角函数在Rt△CFE中求出EF的长,据此进一步计算即可得出答案.
(1)证明:

如图,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)证明:
∵![]() 为直径,
为直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵![]() ,
,
∴△BFG为直角三角形,
∵在Rt△BFG中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在Rt△CFE中:![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
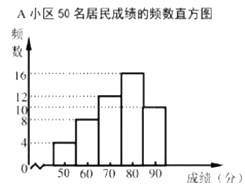
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下
+1,给出定义如下
我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)
(1)通过计算判断数对“﹣2,1”,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m” “共生有理数对”(填“是”或“不是”),并说明理由;
(4)若(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知第一象限内的点
中,已知第一象限内的点![]() 在反比例函数y=
在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,连接
的图象上,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
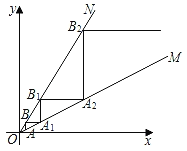
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com