
如图,△ABC中,∠ACB=90°,sinA=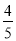 , BC=8,D是AB中点,过点B作直线CD的垂线,垂足为E.
, BC=8,D是AB中点,过点B作直线CD的垂线,垂足为E.

(1)求线段CD的长;
(2)求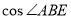 的值.
的值.
(1)5;(2)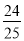 .
.
【解析】
试题分析:(1)由sinA=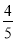 , BC=8,可以求出AB=10,再由直角三角形斜边上的中线等于斜边的一半,求出CD的长;
, BC=8,可以求出AB=10,再由直角三角形斜边上的中线等于斜边的一半,求出CD的长;
(2)过点C作CF⊥AB于F,则有∠ABE=∠DCF,由面积公式求出CF,则容易求出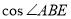 的值.
的值.
试题解析:(1)∵△ABC中,∠ACB=90°,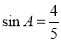 , BC=8,∴
, BC=8,∴ .∵△ABC中,∠ACB=90°,D是AB中点,∴
.∵△ABC中,∠ACB=90°,D是AB中点,∴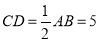 ;
;
(2)过点C作CF⊥AB于F,如图,∴∠CFD=90°.在Rt△ABC中,由勾股定理得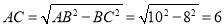 .∵
.∵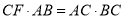 ,∴
,∴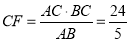 .∵BE⊥CE,∴∠BED=90°.∵∠BDE=∠CDF,∴∠ABE=∠DCF.∴
.∵BE⊥CE,∴∠BED=90°.∵∠BDE=∠CDF,∴∠ABE=∠DCF.∴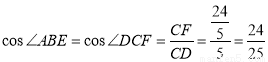 .
.

考点:1.解直角三角形;2.直角三角形斜边上的中线.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:2014-2015学年北京市通州区九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知反比例函数图象经过点(-1,3),那么这个反比例函数的表达式为_______________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
阅读下面材料:
(1)小乔遇到了这样一个问题:如图1,在Rt△ABC中,∠C=90°,D,E分别为CB,CA边上的点,且AE=BC,BD=CE,BE与AD的交点为P,求∠APE的度数;
小乔发现题目中的条件分散,想通过平移变换将分散条件集中,如图2,过点B作BF//AD且BF=AD,连接EF,AF,从而构造出△AEF与△CBE全等,经过推理和计算能够使问题得到解决(如图2).请回答:∠APE的度数为___________________.
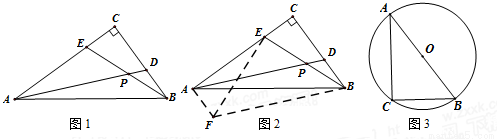
参考小乔同学思考问题的方法,解决问题:
(2)如图3,AB为⊙O的直径,点C在⊙O上,D、E分别为CB,CA上的点,且AE= BC,BD=
BC,BD= CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,反比例函数
中,反比例函数 的图象经过点
的图象经过点 ,
, .
.
(1)求代数式mn的值;
(2)若二次函数 的图象经过点B,求代数式
的图象经过点B,求代数式 的值;
的值;
(3)若反比例函数 的图象与二次函数
的图象与二次函数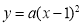 的图象只有一个交点,且该交点在直线
的图象只有一个交点,且该交点在直线 的下方,结合函数图象,求
的下方,结合函数图象,求 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:选择题
已知点A( ,
, ),B(
),B(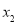 ,
,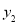 )是反比例函数
)是反比例函数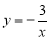 的图象上的两点,若
的图象上的两点,若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.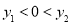 B.
B.
C. D.
D.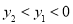
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:填空题
在平面直角坐标系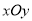 中,对于点
中,对于点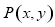 ,其中
,其中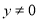 ,我们把点
,我们把点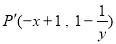 叫做点P的衍生点.已知点
叫做点P的衍生点.已知点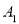 的衍生点为
的衍生点为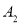 ,点
,点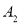 的衍生点为
的衍生点为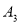 ,点
,点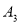 的衍生点为
的衍生点为 ,…,这样依次得到点
,…,这样依次得到点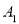 ,
,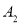 ,
,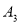 ,…,
,…,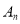 ,…,如果点
,…,如果点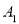 的坐标为
的坐标为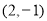 ,那么点
,那么点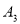 的坐标为________;如果点
的坐标为________;如果点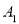 的坐标为
的坐标为 ,且点
,且点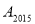 在双曲线
在双曲线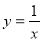 上,那么
上,那么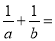 ________.
________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,二次函数y=a(x﹣h)2+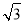 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
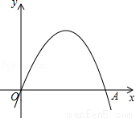
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com