
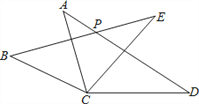
【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为 __________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____(填写符合要求的序号)
(1)两个有理数的和为负数时,这两个数都是负数;
(2)如果两个数的差是正数,那么这两个数都是正数;
(3)几个有理数相乘,当负因数个数为奇数时,乘积一定为负;
(4)数轴上到原点的距离为3的点表示的数是3或﹣3;
(5)0乘以任何数都是0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,画一个长和宽分别为![]() 、
、![]() 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.

![]() 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体?
![]() 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家高斯在上学时曾经研究过这样一个问题,![]() ?
?
经过研究,这个问题的一般性结论是![]() ,其中
,其中![]() 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题:![]() ?
?
观察下面三个特殊的等式:
![]()
![]()
![]()
将这三个等式的两边相加,可以得到![]() .
.
读完这段材料,请你计算:
(1)![]() ________;(直接写出结果)
________;(直接写出结果)
(2)![]() ;(写出计算过程)
;(写出计算过程)
(3)![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )

A. A区 B. B区 C. A区或B区 D. C区
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.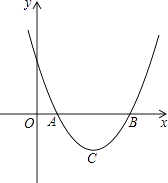
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com