
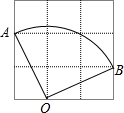
 如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$. 科目:初中数学 来源: 题型:填空题
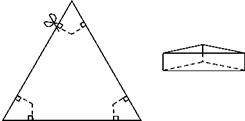 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
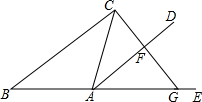 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
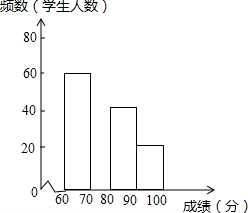 在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:| 成绩 | 频数 | 频率 |
| 60≤x<70 | 60 | 0.30 |
| 70≤x<80 | m | 0.40 |
| 80≤x<90 | 40 | n |
| 90≤x≤100 | 20 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
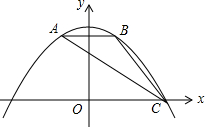 如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数y=$\frac{4}{x}$.
已知反比例函数y=$\frac{4}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
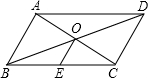 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )| A. | OE=$\frac{1}{2}$DC | B. | OA=OC | C. | ∠BOE=∠OBA | D. | ∠OBE=∠OCE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com