
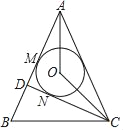
【题目】如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点,⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°;
(2)若NC=3,BC=2![]() ,求DM的长.
,求DM的长.
【答案】(1)∠AOC=135°;(2)DM=1.
【解析】
(1)如图,作OE⊥AC于E,连接OM,ON,由切线的性质可得OM⊥AB,ON⊥CD,由角平分线的性质可得OM=OE,从而得AC是⊙O的切线,继而可得OC平分∠ACD,继而通过推导即可证得∠AOC=135°;
(2)由切线长定理可得AM=AE,DM=DN,CN=CE=3,设DM=DN=x,AM=AE=y,则有BD=3﹣x,在Rt△BDC中,利用勾股定理进行求解即可.
(1)如图,作OE⊥AC于E,连接OM,ON,
∵⊙O与AB相切于点M,与CD相切于点N,
∴OM⊥AB,ON⊥CD,
∵OA平分∠BAC,OE⊥AC,
∴OM=OE,
∴AC是⊙O的切线,
∵ON=OE,ON⊥CD,OE⊥AC,
∴OC平分∠ACD,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠AOC=180°﹣![]() (∠DAC+∠ACD)=180°﹣45°=135°.
(∠DAC+∠ACD)=180°﹣45°=135°.
(2)∵AD,CD,AC是⊙O的切线,M,N,E是切点,
∴AM=AE,DM=DN,CN=CE=3,设DM=DN=x,AM=AE=y,
∵AB=AC,
∴BD=3﹣x,
在Rt△BDC中,∵BC2=BD2+CD2,
∴20=(3﹣x)2+(3+x)2,
∵x>0,
∴x=1,
∴DM=1.


科目:初中数学 来源: 题型:
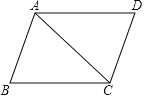
【题目】如图,四边形ABCD 是平行四边形,AB=c,AC=b,BC=a,抛物线 y=ax2+bx﹣c 与 x 轴的一个交点为(m,0).
(1)若四边形ABCD是正方形,求抛物线y=ax2+bx﹣c的对称轴;
(2)若 m=![]() c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出反比例函数y=-![]() 的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=8,BO=10.求:
(1)⊙O的半径;
(2)弦AC的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
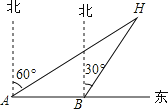
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
A.60 B.30 C.15 D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
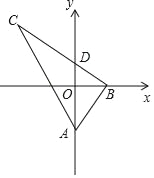
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是太阳能电池板支撑架的截面图,其中AB=300cm,AB的倾斜角为30°,BE=CA=50cm,FE⊥AB于点E.点D、F到地面的垂直距离均为30cm,点A到地面的垂直距离为50cm.求CD和EF的长度各是多少cm(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
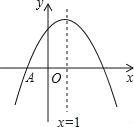
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com