
【题目】如图,某中学一幢教学楼的顶部竖有一块写有“校训”的宣传牌![]() ,
,![]() 米,王老师用测倾器在
米,王老师用测倾器在![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() ,再向教学楼前进9米到达
,再向教学楼前进9米到达![]() 点,测得点
点,测得点![]() 的仰角为
的仰角为![]() ,若测倾器的高度
,若测倾器的高度![]()
![]()
![]() 米,不考虑其它因素,求教学楼
米,不考虑其它因素,求教学楼![]() 的高度.(结果保留根号)
的高度.(结果保留根号)

【答案】教学楼DF的高度为![]() .
.
【解析】
延长AB交CF于E,先证明四边形AMFE是矩形,求出EF=AM=3,再设DE=x米,利用Rt△BCE得到AE=x+12,再根据Rt△ADE得到![]() ,即可得到x的值,由此根据DF=DE+EF求出结果.
,即可得到x的值,由此根据DF=DE+EF求出结果.
如图,延长AB交CF于E,
由题意知:∠DAE=30![]() ,∠CBE=45
,∠CBE=45![]() ,AB=9米,四边形ABNM是矩形,
,AB=9米,四边形ABNM是矩形,
∵四边形ABNM是矩形,
∴AB∥MN,
∵CF⊥MN,
∴∠AEC=∠MFC=90![]() ,
,
∵∠AMF=∠MFC=∠AEF=90![]() ,
,
∴四边形AMFE是矩形,
∴EF=AM=3,
设DE=x米,
在Rt△BCE中, ∠CBE=45![]() ,∴BE=CE=x+3,
,∴BE=CE=x+3,
∵AB=9,
∴AE=x+12,
在Rt△ADE中,∠DAE=30![]() ,∴
,∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴DF=DE+EF=![]() (米).
(米).


科目:初中数学 来源: 题型:
【题目】列方程解应用题
据了解,2019年世园会园区整体结构布局是“一心两轴三带多片区”.“一心”为核心景观区,包括中国馆、国际馆、演艺中心、中国展园和部分世界展园;“两轴”以冠帽山、海坨山为对景,形成正南北向的山水园艺轴和近东西向的世界园艺轴;“三带”包括妫河生态休闲带、园艺生活体验带和园艺产业发展带.为保障2019年世园会的顺利举办,各场馆建设与室内设计都在稳步推进.周末,小明约了几位好友到距离家10千米的场馆路边查看工程进度情况,一部分人骑自行车先走,过了![]() 小时,其余的人乘公交车出发,结果他们同时到达,已知汽车的速度是骑自行车人速度的2倍,求骑车学生每小时走多少千米?
小时,其余的人乘公交车出发,结果他们同时到达,已知汽车的速度是骑自行车人速度的2倍,求骑车学生每小时走多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() (
(![]() ,1)为函数
,1)为函数![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() )与
)与![]() 的图象的交点.
的图象的交点.
(1)求![]() ;
;
(2)若函数![]() 的图象与
的图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() ,
,![]() ;
;
(3)若![]() ,设当
,设当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE﹣EF﹣FC﹣CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC﹣CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).

(1)当点P在DE上,若S△PBQ=![]() ,求t的值.
,求t的值.
(2)当点P运动到折线EF﹣FC上,且点P又恰好落在射线QK上时,求t的值;
(3)连结PG,当PG∥AB时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个布袋中有红、黄、绿三种颜色的球各一个,从中先摸出一个球,记录下它的颜色,将它放回布袋,搅匀,再摸出一个球,记录下它的颜色.
(1)试用树形图或列表法中的一种列举出这两次摸出球的颜色所有可能的结果;
(2)求两次摸出球中至少有一个绿球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(1)如图1,![]() 内接于半径为4的
内接于半径为4的![]() ,若
,若![]() ,则
,则![]() _______;
_______;

问题探究:
(2)如图2,四边形![]() 内接于半径为6的
内接于半径为6的![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积最大值;
的面积最大值;
解决问题
(3)如图3,一块空地由三条直路(线段![]() 、AB、
、AB、![]() )和一条弧形道路
)和一条弧形道路![]() 围成,点
围成,点![]() 是
是![]() 道路上的一个地铁站口,已知
道路上的一个地铁站口,已知![]()
![]() 千米,
千米,![]() 千米,
千米,![]() ,
,![]() 的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点
的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点![]() 处,另外三个入口分别在点
处,另外三个入口分别在点![]() 、
、![]() 、
、![]() 处,其中点
处,其中点![]() 在
在![]() 上,并在公园中修四条慢跑道,即图中的线段
上,并在公园中修四条慢跑道,即图中的线段![]() 、
、![]() 、
、![]() 、
、![]() ,是否存在一种规划方案,使得四条慢跑道总长度(即四边形
,是否存在一种规划方案,使得四条慢跑道总长度(即四边形![]() 的周长)最大?若存在,求其最大值;若不存在,说明理由.
的周长)最大?若存在,求其最大值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
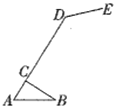
【题目】如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上,量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
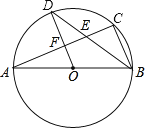
【题目】如图,AB是⊙O的直径,点C、D是⊙O上的点,且OD∥BC,AC分别与BD、OD相交于点E、F.
(1)求证:点D为![]() 的中点;
的中点;
(2)若CB=6,AB=10,求DF的长;
(3)若⊙O的半径为5,∠DOA=80°,点P是线段AB上任意一点,试求出PC+PD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
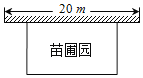
【题目】某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,已知墙长为20米,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com