
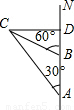
 已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离.
已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离. 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
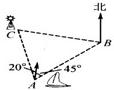 16、如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为
16、如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离.
已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
 B处测得灯塔P在北偏西60°的方向上,已知轮船行驶速度为20千米/时.
B处测得灯塔P在北偏西60°的方向上,已知轮船行驶速度为20千米/时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
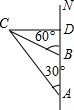 已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离.
已知:如图,上午8时,一条船从A处出发以每小时15海里的速度向正北航行,10时到达B处.从A、B望灯塔C,测得∠NAC=30°,∠NBC=60°,求灯塔C到直线AN的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com