
 如图,图中的小方格都是边长为1的正方形,若A(-x,$\frac{-3y+6}{2}$),B(2x-1,$\frac{2y+1}{3}$),C(z+1,$\frac{2z-8}{3}$),已知A、B关于原点对称,C在二、四象限平分线上.
如图,图中的小方格都是边长为1的正方形,若A(-x,$\frac{-3y+6}{2}$),B(2x-1,$\frac{2y+1}{3}$),C(z+1,$\frac{2z-8}{3}$),已知A、B关于原点对称,C在二、四象限平分线上.分析 (1)根据题目中的信息,可知点A,B的横坐标和纵坐标分别互为相反数,点C的横纵坐标互为相反数,从而可以解得点A、B、C三点的坐标.
(2)根据第(1)问中求得的各点的坐标画出平面直角坐标系.
(3)根据A、B、C三点的坐标,将△ABC放在矩形AEFG中,从而求出相应三角形的面积.
解答 解:(1)∵图中的小方格都是边长为1的正方形,若A(-x,$\frac{-3y+6}{2}$),B(2x-1,$\frac{2y+1}{3}$),C(z+1,$\frac{2z-8}{3}$),已知A、B关于原点对称,C在二、四象限平分线上.
∴$\left\{\begin{array}{l}{-x+2x-1=0}\\{\frac{-3y+6}{2}+\frac{2y+1}{3}=0}\\{z+1+\frac{2z-8}{3}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\\{z=1}\end{array}\right.$.
∴点A的坐标为:(-1,-3),点B的坐标为:(1,3),点C的坐标为:(2,-2).
(2)由点A的坐标为:(-1,-3),点B的坐标为:(1,3),点C的坐标为:(2,-2).
可得A、B、C三点所在的坐标系如下图: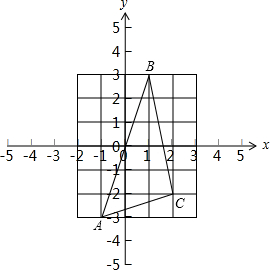
(3)如下图所示: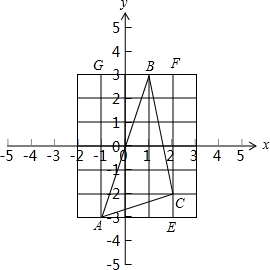
∵点A的坐标为:(-1,-3),点B的坐标为:(1,3),点C的坐标为:(2,-2).
∴S△ABC=S矩形AEFG-S△AEC-S△CFB-S△ABG=$6×3-\frac{3×1}{2}-\frac{1×5}{2}-\frac{2×6}{2}=18-\frac{3}{2}-\frac{5}{2}-6=8$.
点评 本题考查在平面直角坐标系中两点关于原点对称,二四象限角平分线上点的坐标的相关知识,根据各点的坐标可以画出相应的平面之家坐标系,根据三角形各点在平面直角坐标系中的坐标,将△ABC放在矩形AEFG中,从而求出相应三角形的面积.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?
某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com