
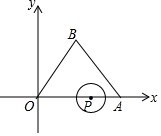
 如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$).
如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$). 分析 当点P在OB上且与边AB相切时,如图,作PH⊥AB于H,则PH=$\sqrt{3}$,根据等边三角形的性质得到∠A=60°,解直角三角形得到AH=$\frac{\sqrt{3}}{3}$PH=1,AP=2AH=2,于是得到结论.
解答 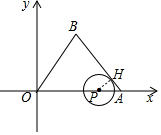 解:当点P在OB上且与边AB相切时,如图,
解:当点P在OB上且与边AB相切时,如图,
作PH⊥AB于H,则PH=$\sqrt{3}$,
∵△ABO为等边三角形,
∴∠A=60°,
在Rt△APH中,AH=$\frac{\sqrt{3}}{3}$PH=1,
AP=2AH=2,
∴OP=6,
∴P(6,0);
∴点P在AO,AP=2时,⊙P与边AB相切,
同理可得点P在OA,OP=2时,⊙P与边BO相切;
点P在OB,BP=2时,⊙P与边OA相切,
点P在OB,BP=2时,⊙P与边AB相切,
则P(3,3$\sqrt{3}$)
点P在AB,BP=2时,⊙P与边BO相切,
点P在AB,AP=2时,⊙P与边OA相切,
综上所述,⊙P运动一圈与△OBC的边相切6次,
故答案为:P(6,0),(3,3$\sqrt{3}$).
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了等边三角形的性质.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
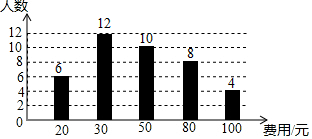 某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )
某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )| A. | 12和10 | B. | 30和50 | C. | 10和12 | D. | 50和30. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
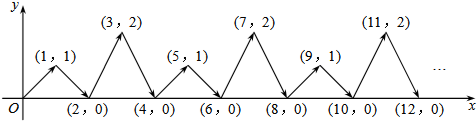
| A. | (2017,0) | B. | (2017,1) | C. | (2017,2) | D. | (2016,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com