Question

19．如图，在平面直角坐标系中，∠ACO=90°，∠AOC=30°，分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE，DF⊥AO于F，连DE交AO于G．
（1）求证：△DFG≌△EOG；
（2）B为AD的中点，连HG，求证：CD=2HG；
（3）在（2）的条件下，AC=4，若M为AC的中点，求MG的长．

Answer 1

分析 （1）根据全等三角形的判定定理AAS证得结论；
（2）如图2，连接AE．构建全等三角形：△DOC≌△AOE（SAS），则该全等三角形的对应边相等DC=AE，所以DC=2HG；
（3）如图2，连接HM．构建等边三角形△HMG．在直角三角形AOC中，AC=4，OD=8，OC=4$\sqrt{3}$；结合等边△AOD的性质可以求得OD的长度；再利用勾股定理不难求得线段CD的长度，则MG=HG=$\frac{1}{2}$CD．

解答 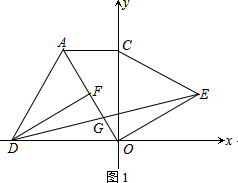证明：（1）如图1，∵∠AOC=30°，
∴∠GOE=90°．
设AC=a，则OA=2a，OE=OC=$\sqrt{3}$a．
在等边△AOD中，DF⊥OA，
∴DF=$\sqrt{3}$a，
∴DF=OE，
∴在△DFG与△EOG中，$\left\{\begin{array}{l}{∠DGF=∠EGF}\\{∠GFD=∠GEO}\\{DF=OE}\end{array}\right.$，
 可证：△DFG≌△EOG（AAS）；

（2）如图2，连接AE．
∵H、G分别为AD、DE的中点，
∴HG∥AE，HG=$\frac{1}{2}$AE．
根据共顶点等腰三角形的旋转模型    可证：△DOC≌△AOE（SAS），
∴DC=AE，
∴DC=2HG；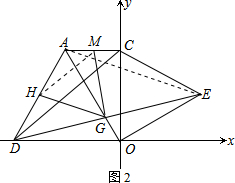

（3）如图2，连接HM．
∵H、M分别为AD、AC的中点，
∴HM=$\frac{1}{2}$CD，
∴HM=HG．
又∠DHG=∠DAE=60°+∠OAE=60°+∠ODC，∠AHM=∠ADC，
∴∠MHG=180°-∠AHM-∠DHG=180°-∠ADC-60°-∠ODC
=120°-（∠ADC-∠ODC）=120°-∠AOD=60°．
∴△HMG为等边三角形，
∵AC=4，
∴OA=OD=8，OC=4$\sqrt{3}$，CD=4$\sqrt{7}$，
∴MG=HG=$\frac{1}{2}$CD=2$\sqrt{7}$．

点评 本题考查了三角形综合题．解答（1）题时，只需要掌握构成全等三角形的条件和全等三角形的判定定理即可解题；解答（2）题时，巧妙的借助于旋转的性质构建全等三角形：△DOC≌△AOE（SAS），这是解题的技巧性所在之处．另外，（3）的辅助线的作法也是值得借鉴的．