
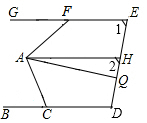
 如图,∠1=∠2.∠GFA=55°,∠ACB=75°,AQ平分∠FAC,AH∥BD,求∠HAQ的度数.
如图,∠1=∠2.∠GFA=55°,∠ACB=75°,AQ平分∠FAC,AH∥BD,求∠HAQ的度数. 分析 先根据∠1=∠2,判定GE∥AH,进而得到GE∥BD,即可得出∠GFA=∠FAH=55°,∠ACB=∠CAH=75°,进而得出∠FAC=55°+75°=130°,根据AQ平分∠FAC,可得∠CAQ=$\frac{1}{2}$∠CAF=65°,即可得出∠HAQ=∠CAH-∠CAQ=10°.
解答 解:∵∠1=∠2,
∴GE∥AH,
又∵AH∥BD,
∴GE∥BD,
∴∠GFA=∠FAH=55°,∠ACB=∠CAH=75°,
∴∠FAC=55°+75°=130°,
∵AQ平分∠FAC,
∴∠CAQ=$\frac{1}{2}$∠CAF=65°,
∴∠HAQ=∠CAH-∠CAQ=75°-65°=10°.
点评 本题主要考查了平行线的性质,角平分线的定义的运用,解题时注意:两直线平行,内错角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
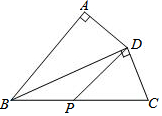 如图,在四边形ABCD中,∠A=90°,AB=7,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为4.
如图,在四边形ABCD中,∠A=90°,AB=7,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC.
看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 5 |
| B型板房 | 78m2 | 41m2 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.| 分数段(分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x≤90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com