
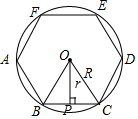
 三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积?
三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积? 分析 经过圆心O作圆的内接正n边形的一边AB的垂线OC,垂足是P,则在直角△OPC中,∠BOC=$\frac{180°}{n}$,弦心距为r,OB即半径R.BC=2PC=a.根据三角函数即可求解.
解答 解:圆内接正六边形可分成六个全等的等边三角形,这样的等边三角形的边长与原正六边形的边长相等,
等边三角形的高与正六边形的边心距相等,
等边三角形的高是它的边长的$\frac{\sqrt{3}}{2}$倍,
所以a:R:r=2:2:$\sqrt{3}$.
正六边形的边长为:6a,
正六边形的面积为:6×$\frac{1}{2}$×ra=3ar.
点评 本题考查了圆内接正六边形的边长,半径,边心距的关系,正确掌握正六边形的性质是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
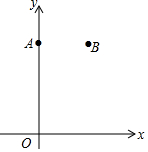 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com