
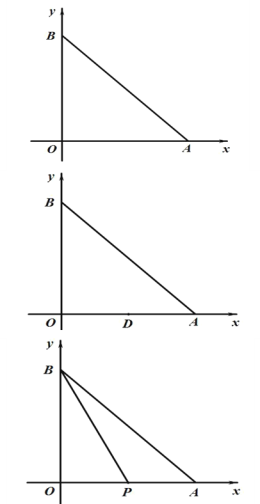
【题目】已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),AB=6![]() ,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
(1)求点 B 的坐标;
(2)设点 P 的运动时间为点 t 秒,△BDP 的面积为 S,求 S 与 t 的函数关系式;
(3)当点 P 与点 D 重合时,连接 BP,点 E 在线段 AB 上,连接 PE,当∠BPE=2∠OBP 时, 求点 E 的坐标.
【答案】(1)B(0,6);(2)S=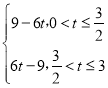 ;(3)E(4,2)
;(3)E(4,2)
【解析】
(1)在Rt△AOB中,利用勾股定理可求得OB的长,从而得到点B的坐标;
(2)存在2种情况,一种是点P在点D的左侧,一种是在右侧,求△PBD的面积,高始终是OB不变,仅需表示出PD的长即可;
(3)如下图,作∠BPE的角平分线PF,根据角之间的关系,可得到PF∥OB,从而推导出△PEG∽△PBO,最后利用相似比的关系求得线段的长度,从而得到E的坐标.
(1)∵A(6,0),AB=6![]() ,△AOB是直角三角形
,△AOB是直角三角形
∴在Rt△AOB中,OB=![]()
∴B(0,6)
(2)情况一:如下图,点P在点D的左侧,即![]() 时
时
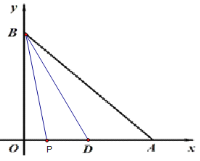
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=3-2t
∴S=![]()
情况二:如下图,点P在点D的右侧,即![]() 时
时
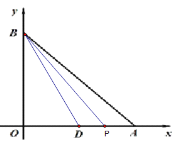
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=2t-3
∴S=![]()
综上得:S=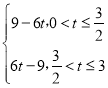
(3)如下图,PF是∠PBE的角平分线,交AB于点F,过点E作x轴的垂线,交x轴于点G
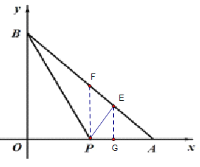
∵OA=6,OB=6,AB=6![]()
∴△OBA是等腰直角三角形,∠A=45°
∴△GEA是等腰直角三角形
设PG=x,则AG=3-x
∴EG=AG=3-x
∵PF是∠BPE的角平分线,∴∠BPF=∠FPE
∵∠BPE=2∠OBP
∴∠OBP=∠BPF=∠FPE
∴PF∥OB,∴PF⊥OA
∴∠FPE+∠EPG=90°
∵∠OBP+∠BPO=90°,∴∠EPG=∠BPO
∵∠EGP=∠BOP
∴△PEG∽△PBO
∴![]() ,即
,即![]() ,解得:x=1
,解得:x=1
∴PG=1,GE=2
∴E(4,2)


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】2019年11月30日上午符离大道正式开通,同时宿州至徐州的K902路城际公交开通试运营,小明先乘K902路城际公交车到五柳站下车,再步行到五柳景区游玩,从出发地到五柳景区全程31千米,共用了1个小时,已知步行的速度每小时4千米,K902路城际公交的速度是步行速度的10倍,求小明乘公交车所行驶的路程和步行的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
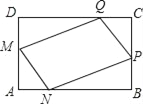
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
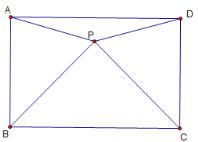
【题目】如图,P 为平行四边形 ABCD 内一点,PB=PC,∠BPC=90°,∠PAB=75°,若 AB=11![]() ,PD=14,则 PA 的长为_______________.
,PD=14,则 PA 的长为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自 2019 年起逐月增加,据统计,该商城 9 月份销售自行车 64 辆,11 月份销售了 100 辆;
(1)若该商城 9 月至 11 月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共 100 辆,已知 A 型车的进价为每辆 500 元,售价为每辆 700 元,B 型车的进价为每辆 1000 元,售价为每辆 1300 元.假设所购进车辆全部售完,为使利润不低于 26000 元,该商城购进 A 型车不超过多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.
(1)写出y关于x的函数关系式 ;x的取值范围是 .
(2)列表,得
x | … | 1 | 2 | 3 | 4 | … |
y | … |
|
|
|
| … |
在给出的坐标系中描点并连线;
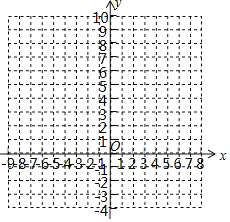
(3)如果A(x1,y1),B(x2,y2)是图象上的两个点,且x1>x2>0,试判断y1,y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点![]() 的坐标为_______.
的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
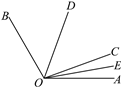
【题目】已知∠AOC和∠BOC,OD平分∠BOC,OE平分∠AOC.
(1)请写出一对相等的角;
(2)若∠AOC在∠BOC的外部,且∠AOB=120°,如图,其他条件不变,求∠EOD的度数.从结果你能看出∠EOD与∠AOB有什么数量关系吗?
(3)若∠AOC=α,∠BOC=β(α,β都大于0°且小于180°,且α<β),其他条件不变,试求∠EOD的度数(结果用含α,β的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com