
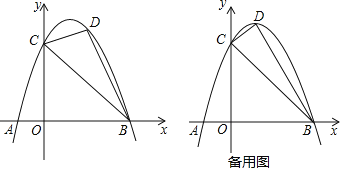
【题目】如图,二次函数![]() 的图象交x轴于A、B两点
的图象交x轴于A、B两点![]() 其中点A在点B的左侧
其中点A在点B的左侧![]() ,交y轴正半轴于点C,且
,交y轴正半轴于点C,且![]() ,点D在该函数的第一象限内的图象上.
,点D在该函数的第一象限内的图象上.
![]() 求点A、点B的坐标;
求点A、点B的坐标;
![]() 若
若![]() 的最大面积为
的最大面积为![]() 平方单位,求点D的坐标及二次函数的关系式;
平方单位,求点D的坐标及二次函数的关系式;
![]() 若点D为该函数图象的顶点,且
若点D为该函数图象的顶点,且![]() 是直角三角形,求此二次函数的关系式.
是直角三角形,求此二次函数的关系式.
【答案】(1)![]() 、
、![]() ;(2)
;(2)![]() ;(3)二次函数表达式为:
;(3)二次函数表达式为:![]() 或
或![]() .
.
【解析】
(1)函数的对称轴为:![]() ,
,![]() ,即可求解;
,即可求解;
(2)由![]() ,即可求解;
,即可求解;
(3)分![]() 两种情况,求解即可.
两种情况,求解即可.
解:![]() 函数的对称轴为:
函数的对称轴为:![]() ,
,![]() ,
,
![]() 点A、B的坐标为
点A、B的坐标为![]() 、
、![]() ;
;
![]() 二次函数表达式为:
二次函数表达式为:![]() ,即:
,即:![]() ,
,
把点B、C坐标代入一次函数表达式![]() 得:
得:![]() ,
,
则一次函数表达式为:![]() ,
,
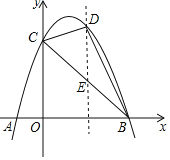
过点D作x轴的平行线交BC于E点,
设点D的坐标为![]() ,则点E的坐标为
,则点E的坐标为![]() ,
,
![]() ,
,
![]() ,故
,故![]() 有最大值,
有最大值,
当![]() 时,最大值为
时,最大值为![]() ,
,
解得:![]() ,
,
点D的坐标为![]() ,
,
故:二次函数表达式为:![]() ;
;
![]() 点B、C、D的坐标分别为
点B、C、D的坐标分别为![]() 、
、![]() ,
,
则直线CD所在直线表达式中的k值为:![]() ,
,
同理![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,
由两直线垂直k值互为负倒数得:![]() ,解得:
,解得:![]() 正值已舍去
正值已舍去![]() ,
,
![]() 当
当![]() 时,同理解得:
时,同理解得:![]() ,
,
故:二次函数表达式为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
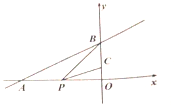
【题目】如图,在平面直角坐标系中,直线![]() 不经过第四象限,且与
不经过第四象限,且与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,其坐标为
上,其坐标为![]() ,连结
,连结![]() ,
,![]() ,若
,若![]() ,那么
,那么![]() 的值为( )
的值为( )
A. ![]() B. 4C. 5D. 6
B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
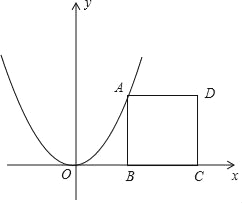
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是关于x的函数,如果能在其函数图象上能找到横坐标与纵坐标相同的一个点P(t,t),则称点P为函数图象上的“郡点”.例如:直线y=2x-1上存在“郡点”P(1,1).
(1)直线y=3x-4的郡点是______;双曲线y=![]() 上的郡点是______.
上的郡点是______.
(2)若抛物线y=x2+5x-5上有“郡点”,且“郡点”A、B(点A,B可重合)的坐标分别为(x1,y1),(x2,y2),求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
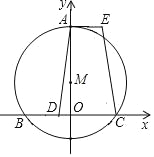
【题目】如图,在平面直角坐标系中,已知点M的坐标为(0,2),以M为圆心,以4为半径的圆与x轴相交于点B、C,与y轴正半轴相交于点A过A作AE∥BC,点D为弦BC上一点,AE=BD,连接AD,EC.
(1)求B、C两点的坐标;
(2)求证:AD=CE;
(3)若点P是弧BAC上一动点(P点与A、B点不重合),过点P的⊙M的切线PG交x轴于点G,若△BPG为直角三角形,试求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
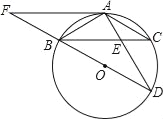
【题目】如图,△ABC为圆O的内接三角形,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
(1)求证:△ABE∽△ADB,并求AB的长;
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(![]() ≈1.7)
≈1.7)
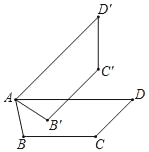
A. 21cmB. 42cmC. 51cmD. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”,我市中小学每年都要举办一届科技运动会,下图为我市某校今年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:

(1)该校参加车模、建模比赛的人数分别是 人和 人:
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 ,并把条形统计图补充完整.
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖,今年我市中小学参加航模比赛人共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com