
 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,求△BEQ周长的最小值?
如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,求△BEQ周长的最小值? 分析 由正方形的性质得出点B与点D关于直线AC对称,得出DE的长即为DQ+QE的最小值,由勾股定理求出DE,即可得出结果.
解答 解:连接DQ,如图所示: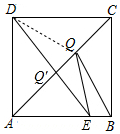
∵EB=AB-AE=1是定值,
∴QE+QB最小时,△QBE的周长最小,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴QE+QB=QE+DQ,
∴当D、Q、E共线时,DQ+QE最小,最小值为DE,
∵∠DAE=90°,AB=AD=4,AE=3,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴QB+QE的最小值为DE,最小值为5,
∴△BEQ的最小值=5+1=6.
点评 本题考查了正方形的性质、最小值问题、勾股定理、轴对称的性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
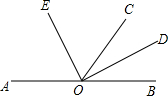 如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
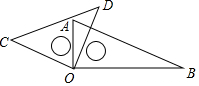 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA与∠DOA互余 | D. | ∠AOD与∠COB互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
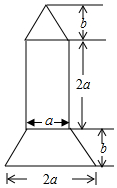 2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,.
2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
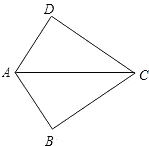 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BAC=∠DAC | ||
| C. | ∠BCA=∠DCA | D. | ∠B=∠D=90°,∠DAC=56°,∠BCA=34° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
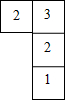 若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.
若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com