
【题目】已知△ABC的周长是20,三边分别为a,b,c.
(1)若b是最大边,求b的取值范围;
(2)若△ABC是三边均不相等的三角形,b是最大边,c是最小边,且b=3c,a,b,c均为整数,求△ABC的三边长.
【答案】(1) ![]() ≤b<10; (2) a=8,b=9,c=3.
≤b<10; (2) a=8,b=9,c=3.
【解析】
(1)根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边即可求解.三角形的任意两边的和大于第三边,已知三边和周长,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;
(2)根据(1)中求出的b的取值范围,结合b为整数,得出b=7,8,9,又b=3c,c为整数,得出b=9,c=3,然后根据△ABC的周长是20求出a的长.
(1)依题意有b≥a,b≥c,又a+c>b,
则a+b+c≤3b且a+b+c>2b,
得2b<20≤3b,
得![]() ≤b<10;
≤b<10;
(2)∵![]() ≤b<10,b为整数,
≤b<10,b为整数,
∴b=7,8,9,
∵b=3c,c为整数,
∴b=9,c=3,
∴a=20-b-c=8.
故△ABC的三边长为c=3,a=8,b=9.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() ,把一条长为2016个单位长度且没有弹性的细线
,把一条长为2016个单位长度且没有弹性的细线![]() 线的粗细忽略不计
线的粗细忽略不计![]() 的一端固定在点A处,并按
的一端固定在点A处,并按![]() 的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是![]()
![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,下列说法:四边形ACED是平行四边形,△BCE是等腰三角形,四边形ACEB的周长是10+2![]() ,④四边形ACEB的面积是16.
,④四边形ACEB的面积是16.
正确的个数是 ( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在八次数学测试中,甲、乙两人的成绩如下:
甲:89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人的极差;并说明谁的成绩变化范围大;
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9,10环的子弹数因被墨水污染而看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发):
甲

乙

(1)求甲同学在这次测验中平均每发射中的环数;
(2)根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.(结果保留到小数点后1位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y1=tx2﹣1(t>0)和抛物线C2:y2=﹣4(x﹣h)2+1(h≥1).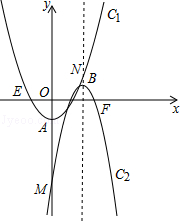
(1)两抛物线的顶点A、B的坐标分别为和;
(2)设抛物线C2的对称轴与抛物线C1交于点N,则t为何值时,A、B、M、N为顶点的四边形是平行四边形.
(3)设抛物线C1与x轴的左交点为点E,抛物线C2与x轴的右边交点为点F,试问,在第(2)问的前提下,四边形AEBF能否为矩形?若能,求出h值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去.

(1)填空:当小王撕了3次后,共有________张纸片;
(2)填空:当小王撕了n次后,共有________张纸片.(用含n的代数式表示)
(3)小王说:我撕了若干次后,共有纸片2013张,小王说的对不对?若不对,请说明你的理由;若对的,请指出小王需撕多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.
(1)求B处到小岛C的距离
(2)若轮船从B处继续向东方向航行,有无触礁危险?请说明理由.
(参考数据: ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
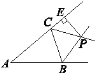
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com