
| 2 | 3 |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:2004年上海市奉贤区中考数学二模试卷(解析版) 题型:填空题
 x+4平行,该正比例函数y随x的增大而 .
x+4平行,该正比例函数y随x的增大而 .查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
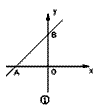
如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足 . . |
| (1)判断△AOB的形状. |
 |
(2)如图②,正比例函数 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长. 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长. |
 |
| (3)如图③,E为AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连结PD、PO,试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明. |
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com