
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
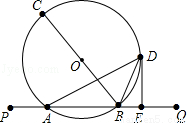
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.
(1)证明:连结OD,如图,
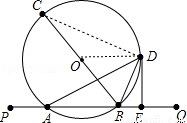
∵BD平分∠CBQ交⊙O于点D,
∴∠CBD=∠QBD,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠QBD,
∴OD∥BQ,
∵DE⊥PQ,
∴OD⊥DE,
∴DE与⊙O相切;
(2)【解析】
∵BC是⊙O的直径,
∴∠BDC=90°,
∵DE⊥AB,
∴∠BED=90°,
∵∠CBD=∠QBD,
∴Rt△BCD∽△BDE,
∴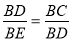 ,即
,即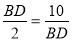 ,
,
∴BD=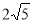 ,
,
在Rt△BCD中,sin∠C=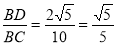 ,
,
∵∠BAD=∠C,
∴sin∠BAD=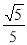 .
.
【解析】
试题分析:(1)连结OD,利用角平分线的定义得∠CBD=∠QBD,而∠OBD=∠ODB,则∠ODB=∠QBD,于是可判断OD∥BQ,由于DE⊥PQ,根据平行线的性质得OD⊥DE,则可根据切线的判定定理得到DE与⊙O相切;
(2)连结CD,根据圆周角定理由BC是⊙O的直径得到∠BDC=90°,再证明Rt△BCD∽△BDE,利用相似比可计算出BD=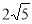 ,在Rt△BCD中,根据正弦的定义得到sin∠C=
,在Rt△BCD中,根据正弦的定义得到sin∠C=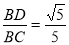 ,然后根据圆周角定理得∠BAD=∠C,即有sin∠BAD=
,然后根据圆周角定理得∠BAD=∠C,即有sin∠BAD=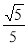
考点:切线的判定;锐角三角函数的定义


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源:2014-2015学年浙江省温州市九年级上学期期中测试数学试卷(解析版) 题型:填空题
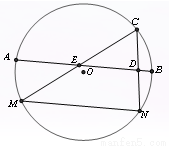
如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为1200,点C是圆O上一个动点(不与M、N重合)。连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B。已知圆O的半径为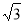 ,那么在点C的运动过程中AE+BD的最小值为 。
,那么在点C的运动过程中AE+BD的最小值为 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市岳池县白庙责任区九年级12月联考数学试卷(解析版) 题型:解答题
(12分)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3。

(1)求抛物线所对应的函数解析式;(3分)
(2)求△ABD的面积;(3分)
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由。(6分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市岳池县白庙责任区九年级12月联考数学试卷(解析版) 题型:选择题
岑溪市重点打造的天龙顶山地公园在2013年12月27日试业了。在此之前,公园派出小曾等人到某旅游景区考察,了解到该景区三月份共接待游客20万人次,五月份共接待游客50万人次。小曾想知道景区每月游客的平均增长率x的值,应该用下列哪一个方程来求出?( )
A.20(1+x) =50 B.20(1﹣x)
=50 B.20(1﹣x) =50
=50
C.50(1+x) =20 D.50(1﹣x)
=20 D.50(1﹣x) =20
=20
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市岳池县白庙责任区九年级12月联考数学试卷(解析版) 题型:选择题
下列成语所描述的事件是必然发生的是( )
A.水中捞月 B.拔苗助长 C.守株待兔 D.瓮中捉鳖
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
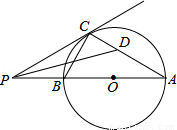
下列结论正确的是 (写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC= BC;
BC;
③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市八年级上学期期末考试数学试卷(解析版) 题型:解答题
(12分)某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
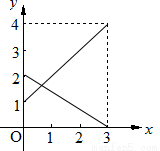
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com