
【题目】如图,O为∠MBN角平分线上一点,⊙O与BN相切于点C,连结CO并延长交BM于点A,过点A作AD⊥BO于点D.
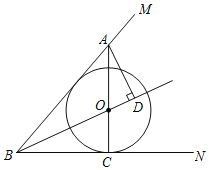
(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)AD=2![]() .
.
【解析】
(1)作OE⊥AB,先由∠AOD=∠BAD求得∠ABD=∠OAD,再由∠BCO=∠D=90°及∠BOC=∠AOD求得∠OBC=∠OAD=∠ABD,最后证△BOC≌△BOE得OE=OC,依据切线的判定可得;
(2)先求得∠EOA=∠ABC,在Rt△ABC中求得AC=8,AB=10,由切线长定理知BE=BC=6,AE=4,OE=3,继而得BO=3![]() ,根据相似三角形的性质即可得出结论.
,根据相似三角形的性质即可得出结论.
解:(1)过点O作OE⊥AB于点E,
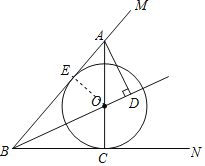
∵O为∠MBN角平分线上一点,
∴∠ABD=∠CBD,
又∵BC为⊙O的切线,
∴AC⊥BC,
∵AD⊥BO于点D,
∴∠D=90°,
∴∠BCO=∠D=90°,
∵∠BOC=∠AOD,
∴∠BAD+∠ABD=90°,∠AOD+∠OAD=90°,
∵∠AOD=∠BAD,
∴∠ABD=∠OAD,
∴∠OBC=∠OAD=∠ABD,
在△BOC和△BOE中,
∵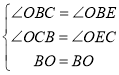 ,
,
∴△BOC≌△BOE(AAS),
∴OE=OC,
∵OE⊥AB,
∴AB是⊙O的切线;
(2)∵∠ABC+∠BAC=90°,∠EOA+∠BAC=90°,
∴∠EOA=∠ABC,
∵tan∠ABC=![]() 、BC=6,
、BC=6,
∴AC=BCtan∠ABC=8,
则AB=10,
由(1)知BE=BC=6,
∴AE=4,
∵tan∠EOA=tan∠ABC=![]() ,
,
∴![]() ,
,
∴OE=3,OB=![]() =3
=3![]() ,
,
∵∠ABD=∠OBC,∠D=∠ACB=90°,
∴△ABD∽△OBC,
∴![]() ,即
,即![]() ,
,
∴AD=2![]() .
.
故答案为:AD=2![]() .
.


科目:初中数学 来源: 题型:
【题目】下面的方格纸中,画出了一个“小老鼠”的图案,已知每个小正方形的边长为1
(1)在上面的方格纸中作出“小老鼠”关于直线DE对称的图案(只画图,不写作法).
(2)以G为原点,GE所在直线为x轴,GH所在直线为y轴,小正方形的边长为单位长度建立直角坐标系,问:是否存在以点Q为顶点,且过点H和E的抛物线,并通过计算说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=12,CE=3时,求AC的长.
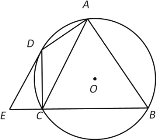
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是我市全面推进中小学校“社会主义核心价值观”教育年.某校对全校学生进行了中期检测评价,检测结果分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表(图1)和统计图(图2).
(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表(图1)和统计图(图2).
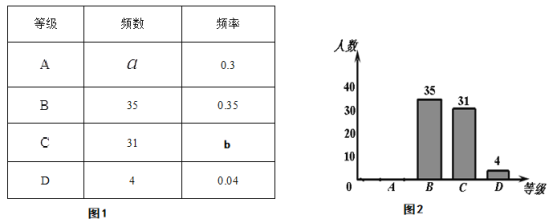
请根据图1、图2提供的信息,解答下列问题:
(1)本次随机抽取的样本容量为
(2)![]() ,
,![]() .
.
(3)请在图2中补全条形统计图.
(4)若该校共有学生800人,据此估算,该校学生在本次检测中达到“![]() (优秀)”等级的学生人数为 人.
(优秀)”等级的学生人数为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )

A.2B.4C.5﹣![]() D.8﹣2
D.8﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中
中![]() .点
.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,以
运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,当直线
运动,当直线![]() 和正方形
和正方形![]() 开始有公共点时,点
开始有公共点时,点![]() 运动的时间为__________
运动的时间为__________![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
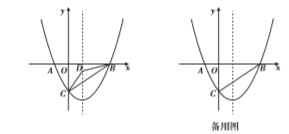
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com