
如图,在等腰梯形ABCD中,AD∥BC.O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H.已知⊙O与AB边相切,切点为F
(1)求证:OE∥AB;
(2)求证:EH=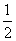 AB;
AB;
(3)若AD与⊙O也相切,如图二,已知BE(BC)=5,BH=3,求⊙O的半径
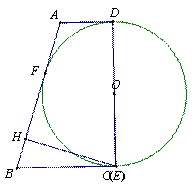
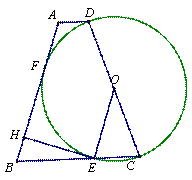
 图一 图二
图一 图二
(1)∵ABCD是等腰梯形 ∴∠B=∠C (1分)
 ∵OE=OC ∴∠OEC=∠C (1分)
∵OE=OC ∴∠OEC=∠C (1分)
∴∠OEC=∠B ∴OE∥AB (1分)
(2)连结OF
∵AB与⊙O相切与点F ∴∠OFB=90°(1分)
又∵EH⊥AB ,OE∥AB
∴∠OEH=∠EHF=90°
∴四边形OFHE是矩形 (1分)
∵OE=OF
∴四边形OFH E是正方形 (1分)
E是正方形 (1分)
∴EH=OE=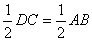 (1分)
(1分)
 (3)连结OF、OB
(3)连结OF、OB
∵AD与圆相切
∴∠ADC=90°
∵AD∥BC
∴∠DCB=90°
∵∠OFB=∠OCB=90°,OF=OC ,OB=OB
∴⊿OFB≌⊿OBC
∴BF=BC=5 (1分)
∵BH=3
∴HF=2 ,HC=4
过点 O作OM⊥CH与点M,在⊿OMC中设OC=r
O作OM⊥CH与点M,在⊿OMC中设OC=r
可得r2-(4-r)2=22 (1分)
∴r=2.5 (1分) ∴⊙O半径是2.5


科目:初中数学 来源: 题型:
给出下列四个命题(1)如果某圆锥的侧面展开图是半圆,则其底面直径与母线长相等.(2)若点A在直线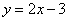 上,且点A到两坐标轴的距离相等,则点A在第一或第四象限.(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个.(4)若A(
上,且点A到两坐标轴的距离相等,则点A在第一或第四象限.(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个.(4)若A(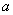 ,
,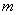 )、B(
)、B(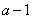 ,
,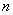 )(
)(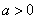 )在反比例函数
)在反比例函数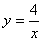 的图象上,则
的图象上,则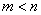 .(5)用反证法证明命题“在一个三角形中,至少有一个内角不小于
.(5)用反证法证明命题“在一个三角形中,至少有一个内角不小于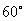 ”,可先假设三角形中每一个内角都小于
”,可先假设三角形中每一个内角都小于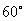 。其中,正确命题的个数是( )
。其中,正确命题的个数是( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
李明在一次测验中做了3道习题,请你判断他是否都正确,若有不正确,请在答题卷相应题号后写上不正确,并写出正确的解答;若正确,则只在答题卷的相应题号后写上“正确”即可。
①化简 =
=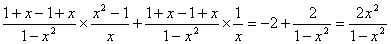
②解不等式组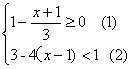 由(1)得
由(1)得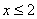 ; 由(2)得
; 由(2)得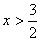 ∴
∴ 
③计算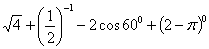 =2+2-1+1=4
=2+2-1+1=4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB//CD,∠ACD=72°﹒
⑴用直尺和圆规作∠C的平分线CE,交AB于E,并在CD上取一点F,使AC=AF,再连接AF,交CE于K;(要求保留作图痕迹,不必写出作法)
⑵依据现有条件,直接写出图中所有相似的三角形﹒(图中不再增加字母和线段,不要求证明)﹒
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com