
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
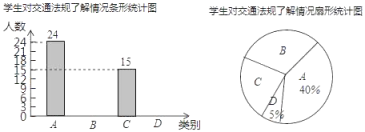
请结合图中所给信息解答下列问题:
(1)本次共调查 名学生;扇形统计图中C所对应扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求丙和丁两名学生同时被选中的概率.
【答案】(1)本次调查的学生总人数为60人,扇形统计图中C所对应扇形的圆心角度数是90°;(2)补全条形图见解析;(3)丙和丁两名学生同时被选中的概率为![]() .
.
【解析】
(1)由A的人数及其所占百分比可得总人数,用360°乘以C人数所占比例即可得;
(2)总人数乘以D的百分比求得其人数,再根据各类型人数之和等于总人数求得B的人数,据此补全图形即可得;
(3)画树状图列出所有等可能结果,再利用概率公式计算可得.
(1)本次调查的学生总人数为24÷40%=60人,扇形统计图中C所对应扇形的圆心角度数是360°×![]() =90°,
=90°,
故答案为60、90°;
(2)D类别人数为60×5%=3,
则B类别人数为60﹣(24+15+3)=18,
补全条形图如下:
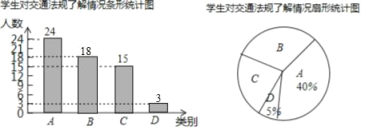
(3)画树状图为:
![]()
共有12种等可能的结果数,其中丙和丁两名学生同时被选中的结果数为2,
所以丙和丁两名学生同时被选中的概率为![]() =
=![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】2019 年3月16日,由中国科协主办的第六届全国青年科普创新实验暨作品大赛启动,重点围绕“智能、环保、教育”三大主题,某中学派出甲、乙两组队伍参加本次大赛,有四个命题供他们选择:
①智能:智能控制及人工智能命题(用![]() 表示)
表示)
②环保:包括生物环境、风能两个命题(分别用![]() 表示)
表示)
③教育:未来教育命题(用![]() 表示)
表示)
![]() 甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
![]() 若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
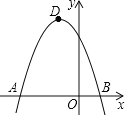
【题目】在平面直角坐标系中,二次函数y=-x2-bx+c的图象经过点A,点B(1,0)和点C(0,3).点D是抛物线的顶点.
(1)求二次函数的解析式和点D的坐标
(2)直线y=kx+n(k≠0)与抛物线交于点M,N,当△CMN的面积被y轴平分时,求k和n应满足的条件
(3)抛物线的对称轴与x轴交于点E,将抛物线向下平移m(m>0)个单位,平移后抛物线与y轴交于点C′,连接DC′,OD,是否存在OD平分∠C′DE的情况?若存在,求出m的值;若不荐在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司以10元/千克的价格收购一批产品进行销售,经过市场调查获悉,日销售量y(千克)是销售价格x(元/千克)的一次函数,部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)直接写出y与x之间的函数表达式;
(2)求日销售利润为150元时的销售价格;
(3)若公司每销售1千克产品需另行支出a元(0<a<10)的费用,当20≤x≤25时,公司的日获利润的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
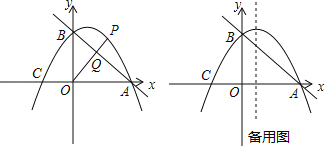
【题目】如图,直线y=﹣![]() x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
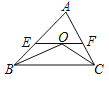
【题目】如图,在![]() 中,
中, ![]() 是
是![]() 平分线的交点,过点O作
平分线的交点,过点O作![]() ,分别交
,分别交![]() 于点
于点![]() ,已知
,已知![]() (
(![]() 常数) ,设
常数) ,设![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,在下列图像中,大致表示
,在下列图像中,大致表示![]() 与
与![]() 之间的函数关系式的是( )
之间的函数关系式的是( )
A.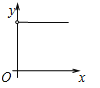 B.
B.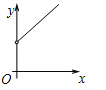 C.
C.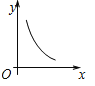 D.
D.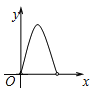
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图像的一支分别交
的图像的一支分别交![]() 于点
于点![]() ,延长
,延长![]() 交反比例函数的图像的另一支于点E,已知D的纵坐标为
交反比例函数的图像的另一支于点E,已知D的纵坐标为![]() .
.
(1)求反比例函数的解析式及直线OA的解析式;
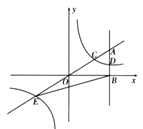
(2)连接BC,已知![]() ,求
,求![]()
(3)若在![]() 轴上有两点
轴上有两点![]() ,将直线
,将直线![]() 绕点
绕点![]() 旋转,仍与
旋转,仍与![]() 交于
交于![]() ,能否构成以
,能否构成以![]() 为顶点的四边形为菱形,如果能请求出
为顶点的四边形为菱形,如果能请求出![]() 的值,如果不能说明理由.
的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】便民”水泥代销点销售某种水泥,每吨进价为250元,如果每吨销售价定为290元时,平均每天可售出16吨.
(1)若代销点采取降低促销的方式,试建立每吨的销售利润y(元)与每吨降低x(元)之间的函数关系式;
(2)若每吨售价每降低5元,则平均每天能多售出4吨,问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com