
【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
【答案】30°或150°.
【解析】
分等边△ADE在正方形的内部和外部两种情况分别求解即可得.
如图1,
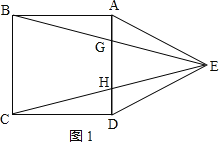
∵四边形ABCD为正方形,△ADE为等边三角形,
∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,
∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,
∴∠AEB=∠CED=15°,
则∠BEC=∠AED﹣∠AEB﹣∠CED=30°;
如图2,
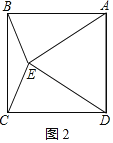
∵△ADE是等边三角形,
∴AD=DE,
∵四边形ABCD是正方形,
∴AD=DC,
∴DE=DC,
∴∠CED=∠ECD,
∴∠CDE=∠ADC﹣∠ADE=90°﹣60°=30°,
∴∠CED=∠ECD=![]() ×(180°﹣30°)=75°,
×(180°﹣30°)=75°,
∴∠BEC=360°﹣75°×2﹣60°=150°,
故答案为:30°或150°.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC. 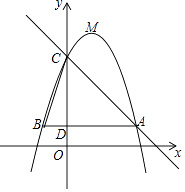
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.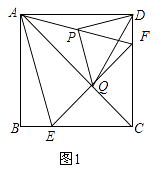
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.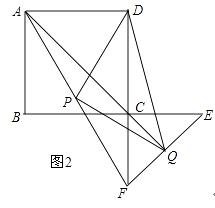
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示. 
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D,F分别在边AC,BC上,易证:AD=BF(不需要证明);
(1)探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD,BF,其他条件不变,如图②,求证:AD=BF;
(2)应用:若α=45°,CD= ![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
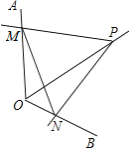
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com