Question

【题目】如图，已知点D在⊙O的直径AB延长线上，点C在⊙O上，过点D作ED⊥AD，与AC的延长线相交于点E，且CD＝DE.

(1)求证：CD为⊙O的切线；

(2)若AB＝12，且BC＝CE时，求BD的长．

Answer 1

【答案】（1）详见解析；（2）6－6.

【解析】

（1）连结0C，由AB为直径，得到∠ACB=90°，求得∠E=∠ABC，根据等腰三角形的性质得到∠ABC=∠OCB，等量代换得到∠E=∠OCB，推出OC⊥CD，于是得到结论；
（2）证明△OBC≌△DCE(ASA),得到OC＝CD＝6，根据勾股定理求出斜边的长，进而可求出BD的长．

(1)证明：连接OC，

∵AB为直径，

∴∠ACB＝90°，

∴∠BCD＋∠ECD＝90°，

在Rt△ADE和Rt△ABC中，∠E＝90°－∠A，∠ABC＝90°－∠A,

∴∠E＝∠ABC，

∵OB＝OC，

∴∠ABC＝∠OCB，

∴∠E＝∠OCB，

又∵CD＝DE，

∴∠E＝∠ECD，

∴∠OCB＝∠ECD，

∴∠OCB＋∠BCD＝90°，即OC⊥CD，

∴CD为⊙O的切线．

(2)由(1)知，∠OBC＝∠OCB＝∠DCE＝∠E，

在△OBC和△DCE中，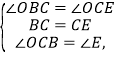

∴△OBC≌△DCE(ASA),

∴OC＝CD＝6，

Rt△OCD中，OC＝CD＝6，∠OCD＝90°，

∴

即