
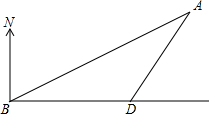
 如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险? 分析 过A作AC⊥BD于点C,求出∠CAD、∠CAB的度数,求出∠BAD和∠ABD,根据等边对等角得出AD=BD=12,根据含30度角的直角三角形性质求出CD,根据勾股定理求出AD即可.
解答 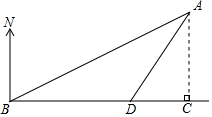 解:只要求出A到BD的最短距离是否在以A为圆心,以8海里的圆内或圆上即可,
解:只要求出A到BD的最短距离是否在以A为圆心,以8海里的圆内或圆上即可,
如图,过A作AC⊥BD于点C,则AC的长是A到BD的最短距离,
∵∠CAD=30°,∠CAB=60°,
∴∠BAD=60°-30°=30°,∠ABD=90°-60°=30°,
∴∠ABD=∠BAD,
∴BD=AD=12海里,
∵∠CAD=30°,∠ACD=90°,
∴CD=$\frac{1}{2}$AD=6海里,
由勾股定理得:AC=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$≈10.392>8,
即渔船继续向正东方向行驶,没有触礁的危险.
点评 考查了勾股定理的应用和解直角三角形,此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
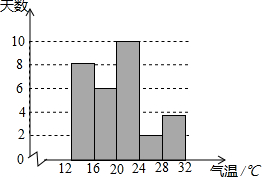 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )| A. | AB=AD | B. | BC=CD | C. | $\widehat{AB}=\widehat{AD}$ | D. | ∠BCA=∠DCA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
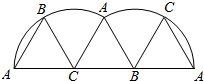 等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.
等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com