
 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.分析 (1)要证明∠P=∠BAC,只要证明∠CAP+∠BAC=∠P+∠CAP即可,根据题目中的条件可以证明它们相等,从而可以解答本题;
(2)要证明直线CD是⊙O的切线,只要证明∠OCD=90°即可,根据题目中的条件和(1)中的结论可以证明∠OCD=90°,从而可以解答本题.
解答 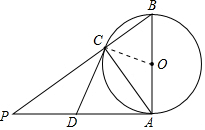 证明:(1)∵AB是⊙O的直径,
证明:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACP=90°,
∴∠P+∠CAP=90°,
∵AP⊙O是切线,
∴∠BAP=90°,
即∠CAP+∠BAC=90°
∴∠P=∠BAC;
(2)∵CD是Rt△PAC斜边PA的中线,
∴CD=AD,
∴∠DCA=∠DAC,
连接OC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠DCO=∠DAO=90°,
∴CD是⊙O的切线.
点评 本题考查切线的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.
如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com