
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
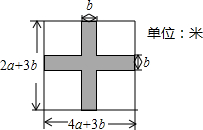 如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 8或10 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形为“等角三角形”.如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D.找出图中的一对“等角三角形”并说明理由.
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形为“等角三角形”.如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D.找出图中的一对“等角三角形”并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
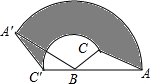 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)| A. | 15π | B. | 60π | C. | 45π | D. | 75π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com