
 与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
与△ABC三边围成的区域有重叠部分,求重叠部分的面积. =1(s)
=1(s) =4(s)
=4(s)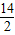 =7(s).
=7(s).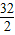 =16(s).
=16(s). π×62=9π(cm2)
π×62=9π(cm2)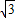 cm,BP=6
cm,BP=6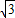 cm,S△POB=
cm,S△POB= ×6
×6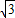 ×3=9
×3=9 (cm2)
(cm2) =6π(cm2)
=6π(cm2) +6π(cm2)
+6π(cm2)


科目:初中数学 来源:2006年福建省泉州市晋江市初中学业质量检查数学试卷(解析版) 题型:解答题
 m.求点B到地面的垂直距离BC.
m.求点B到地面的垂直距离BC.
查看答案和解析>>
科目:初中数学 来源:2005年江苏省南京市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2005年江苏省南京市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2005年江苏省南京市中考数学试卷(解析版) 题型:选择题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com