Question

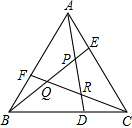
7．△ABC为正三角形，D、E、F三等分BC、AC、AB．如图，则S_△PQR：S_△ABC=$\frac{1}{7}$．

Answer 1

分析 首先根据题意得到△ABE≌△BCF≌△CAD，△AEP≌△BFQ≌△CDR，从而得到PQ=QR=PR，得到△CDR∽△ADC，从而得到DR：DC=DC：DA=RC：CA，作AM⊥BC于点M，设CD=x，则AC=3x，表示出PR和AC，根据△PQR∽△ABC利用相似三角形的面积的比等于相似比的平方即可求得结论．

解答 解：依题意知：△ABE≌△BCF≌△CAD，△AEP≌△BFQ≌△CDR，
∴BE=CF=AD，AP=BQ=CR，PF=FQ=DR，
∴BE-BQ-PE=CF-CR-FQ=AD-AP-DR，
∴PQ=QR=PR，
∴△CDR∽△ADC，
∴DR：DC=DC：DA=RC：CA，
作AM⊥BC于点M，设CD=x，则AC=3x，
在RT△ACM中，AM=ACsin60°=3x×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}x$，CM=$\frac{3}{2}$x，
∴DM=CM-CD=$\frac{3}{2}$x-x=$\frac{1}{2}$x，
在RT△ADM中，AD=$\sqrt{A{M}^{2}+D{M}^{2}}$=$\sqrt{7}$x，
∴$\frac{DR}{DC}$=$\frac{RC}{CA}$=$\frac{DC}{DA}$=$\frac{x}{\sqrt{7}x}$=$\frac{\sqrt{7}}{7}$，
∴DR=$\frac{\sqrt{7}}{7}$DC=$\frac{\sqrt{7}}{7}$x，RC=$\frac{\sqrt{7}}{7}$CA=$\frac{\sqrt{7}}{7}$×3x=$\frac{3\sqrt{7}}{7}$x，
∴PR=AD-AP-RD=$\sqrt{7}$x-$\frac{3\sqrt{7}}{7}$-$\frac{\sqrt{7}}{7}$x=$\frac{3\sqrt{7}}{7}$x，
∵△PQR、△ABC为等边三角形，
∴△PQR∽△ABC，
∴$\frac{{S}_{△PQR}}{{S}_{△ABC}}$=（$\frac{PR}{AC}$）²=（$\frac{\frac{3\sqrt{7}}{7}}{3x}$）²=$\frac{1}{7}$．
故答案为：$\frac{1}{7}$．

点评 本题考查了面积及等积变换的知识，解题的关键是根据题意得到两三角形相似，利用相似三角形的面积的比等于相似比的平方即可求得结论．