练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若根式有意义，则双曲线与抛物线的交点在第　 象限．
    二.

    试题分析：根据题意得，2﹣2k＞0，∴2k﹣2＜0.
    ∴反比例函数的图象位于第二、四象限.
    ∵抛物线的对称轴为直线，与y轴的交点为（0，2﹣2k）在y轴正半轴，
    ∴抛物线的图象不经过第四象限.
    ∴双曲线与抛物线的交点在第二象限.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，已知：为边长是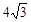的等边三角形，四边形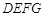为边长是6的正方形. 现将等边和正方形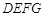按如图①的方式摆放，使点与点重合，点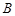、、在同一条直线上，从图①的位置出发，以每秒1个单位长度的速度沿方向向右匀速运动，当点与点重合时暂停运动，设的运动时间为秒（）.

    （1）在整个运动过程中，设等边和正方形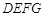重叠部分的面积为，请直接写出与之间的函数关系式；
    （2）如图②，当点与点重合时，作的角平分线交于点，将绕点逆时针旋转，使边与边重合，得到. 在线段上是否存在点，使得为等腰三角形. 如果存在，求线段的长度；若不存在，请说明理由.
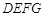    （3）如图③，若四边形为边长是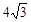的正方形，的移动速度为每秒 个单位长度，其余条件保持不变. 开始移动的同时，点从点开始，沿折线以每秒个单位长度开始移动，停止运动时，点也停止运动. 设在运动过程中，交折线于点，则当时，求的值.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，已知△ABC的三个顶点坐标分别为A（-4，0），B（1，0），C（-2，6）.

    （1）求经过点A，B，C三点的抛物线解析式．
    （2）设直线BC交y轴于点E，连结AE，求证：AE=CE；
    （3）设抛物线与y轴交于点D，连结AD交BC于点F，求证：以A，B，F为顶点的三角形与△ABC相似，并求：．

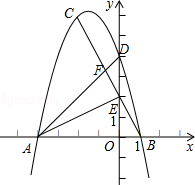
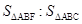    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）。已知E、F在ＡＢ边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).

    （1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；
    （2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？S最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    若将函数的图像向右平行移动1个单位，则它与直线的交点坐标是（   ）
    A．（－3，0）和（5，0）B．（－2，b）和（6，b）
    C．（－2，0）和（6，0）D．（－3，b）和（5，b）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    已知二次函数（m为常数）的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程的两实数根是
    A．x1=1,x2=-2B．x1=1,x2=2C．x1=1,x2=0D．x1=1,x2=3

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    写出一个开口向下、且经过点（-1，2）的二次函数的表达式                ；

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知函数的图象如图所示，则下列结论中：①；②；③；④．正确的是              ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    二次函数的图象的顶点坐标是（    ）
    A．（－1，3）B．（1，3）C．（1，－3）D．（－1，－3）

    查看答案和解析>>

    同步练习册答案