练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

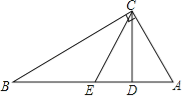
    【题目】如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是（ ）

    A. 60°B. 45°C. 30°D. 75°

    【答案】C

    【解析】

    试题根据轴对称的性质可知∠CED=∠A，根据直角三角形斜边上的中线的性质、等腰三角形的性质可得∠ECA=∠A，∠B=∠BCE，根据等边三角形的判定和性质可得∠CED=60°，再根据三角形外角的性质可得∠B的度数，从而求得答案．

    解：∵在Rt△ABC中，∠ACB=90°，CD为AB边上的高，点A关于CD所在直线的对称点E恰好为AB的中点，

    ∴∠CED=∠A，CE=BE=AE，

    ∴∠ECA=∠A，∠B=∠BCE，

    ∴△ACE是等边三角形，

    ∴∠CED=60°，

    ∴∠B=∠CED=30°．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

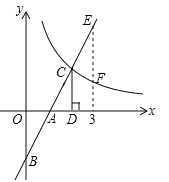
    【题目】（3分）如图，在直角坐标系中，直线与坐标轴交于A、B两点，与双曲线（）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：

    ①；

    ②当0＜x＜3时，；

    ③如图，当x=3时，EF=；

    ④当x＞0时，随x的增大而增大，随x的增大而减小．

    其中正确结论的个数是（ ）

    A．1 B．2 C．3 D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：a、b为有理数，下列说法：①若 a、b互为相反数，则；②若则；③若，则；④若，则是正数.其中正确的有

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点0是AC边上一动点，过点0作DE，使DE∥BC，DE交∠ACB的角平分线于点D，交∠ACB的外角平分线于点E.

    (1)求证：OD=OE；

    (2)当点0运动到何处时，四边形CDAE是矩形?请证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

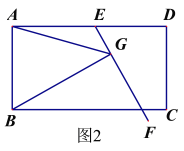
    问题：如图1，在平行四边形ABCD中，E是AD上一点，AE=AB，∠EAB=60°，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG.

    求证：EG =AG+BG.

    小明同学的思路是：作∠GAH=∠EAB交GE于点H，构造全等三角形，经过推理解决问题.

    参考小明同学的思路，探究并解决下列问题：

    （1）完成上面问题中的证明；

    （2）如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG、AG、BG之间的数量关系，并证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心．按此说法，四边形的四个角平分线交于一点，我们也称为“四边形的内心”．

    （1）试举出一个有内心的四边形．

    （2）探究：对于任意四边形ABCD，如果有内心，则四边形的边长具备何种条件？为什么？

    （3）探究：腰长为的等腰直角三角形ABC，∠C=90°，O是△ABC的内心，若沿图中虚线剪开，O仍然是四边形ABDE的内心，此时裁剪线有多少条？

    （4）问题（3）中，O是四边形ABDE内心，且四边形ABDE是等腰梯形，求DE的长？

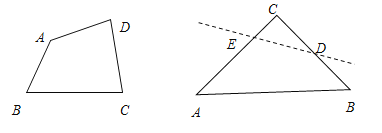
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．

    （1）求证：△ADE≌△FCE．

    （2）若∠BAF=90°，BC=5，EF=3，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在黄州服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周（7天）涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售．

    （1）试建立销售价y与周次x之间的函数关系式；

    （2）若这种时装每件进价Z与周次x次之间的关系为Z=﹣0.125（x﹣8）2+12，1≤x≤16，且x为整数，试问该服装第几周出售时，每件销售利润最大？最大利润为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是边长为6的等边三角形，点D、E分别是边AB、AC的中点，将△ADE绕点A旋转，BD与CE所在的直线交于点F．

    (1)如图(2)所示，将△ADE绕点A逆时针旋转，且旋转角不大于60°，∠CFB的度数是多少？说明你的理由？

    (2)当△ADE绕点A旋转时，若△BCF为直角三角形，求出线段BF的长.

    查看答案和解析>>

    同步练习册答案