
【题目】如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
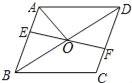
A. 35° B. 55° C. 65° D. 75°
 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ![]() ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a= ![]() 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按规律排列的一列数:
第1个式子:1-![]() ;
;
第2个式子:2-![]() ×
×![]() ×
×![]() ;
;
第3个式子:3-![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() .
.
(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|= 6+7 ;|6-7|=7-6;|7-6|=7- 6;|-6-7|=6+7;
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7-21|= ;
②![]() = ;
= ;
(2)数a在数轴上的位置如图所示,则|a-2.5|=( )
A.a-2.5 B.2.5-a C.a+2.5 D.-a-2.5
![]()
(3)用合理的方法计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
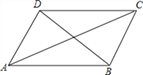
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;
(2)以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;
(3)△A2B2C2的面积是平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两个点A、B所对应的数为a、b,且a、b满足![]() .
.
(1)求AB的长;

(2)若甲、乙分别从A、B两点同时在数轴上相向运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,求甲乙相遇点所表示的数;

(3)若点C对应的数为—1,在数轴上A点的左侧是否存在一点P,使PA+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容![]() 亿立方米,防洪库容
亿立方米,防洪库容![]() 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒![]() ─
─![]() 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.
三峡水电站总装机![]() 万千瓦,年发电量
万千瓦,年发电量![]() 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.
三峡水库回水可改善川江![]() 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的![]() 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由![]() 万吨增加到
万吨增加到![]() 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
思考:
![]() 三峡水电站年发电量
三峡水电站年发电量![]() 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电![]() 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留![]() 个有效数字)
个有效数字)
![]() 宜都市
宜都市![]() 万人,平均一户
万人,平均一户![]() 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC= ![]() .求证:
.求证: 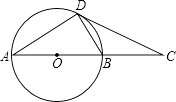
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com