
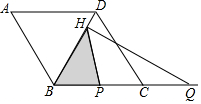
 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )
如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )| A. | 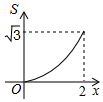 | B. | 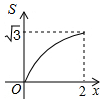 | C. | 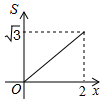 | D. | 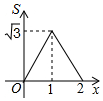 |
分析 根据菱形的性质得到∠DBC=60°,根据直角三角形的性质得到BH=$\frac{1}{2}$BQ=1+$\frac{1}{2}$x,过H作HG⊥BC,得到HG=$\frac{\sqrt{3}}{2}$BH=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{4}$x,根据三角形的面积公式即可得到结论.
解答 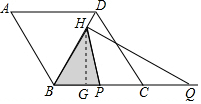 解:∵菱形ABCD的边长为2,∠A=60°,
解:∵菱形ABCD的边长为2,∠A=60°,
∴∠DBC=60°,
∵BQ=2+x,QH⊥BD,
∴BH=$\frac{1}{2}$BQ=1+$\frac{1}{2}$x,
过H作HG⊥BC,
∴HG=$\frac{\sqrt{3}}{2}$BH=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{4}$x,
∴S=$\frac{1}{2}$PB•GH=$\frac{\sqrt{3}}{8}$x2+$\frac{\sqrt{3}}{4}$x,(0<x≤2),
故选A.
点评 本题考查了动点问题的函数图象,菱形的性质,直角三角形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全县的全体八年级学生 | |
| B. | 全县的全体八年级学生期末数学考试成绩 | |
| C. | 抽取的200名学生 | |
| D. | 抽取的200名学生期末数学考试成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
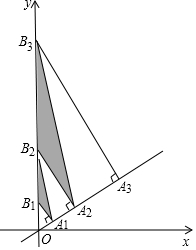 如图,直线y=$\frac{{\sqrt{3}}}{3}$x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,分别过点A1,A2,A3,…An+1作直线y=$\frac{{\sqrt{3}}}{3}$x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为(22n-1-2n-1)$\sqrt{3}$.(用含正整数n的式子表示)
如图,直线y=$\frac{{\sqrt{3}}}{3}$x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,分别过点A1,A2,A3,…An+1作直线y=$\frac{{\sqrt{3}}}{3}$x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为(22n-1-2n-1)$\sqrt{3}$.(用含正整数n的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com