
分析 (1)根据每增加1件,购买的所有服装的单价降低2元,由此即可解决.
(2)分①0≤x≤10,②10<x≤25,③x>25,分别求出y与x的关系即可.
(3)根据(2)中结论列出方程即可解决,注意自变量的取值范围.
解答 解:(1)由题意x=12时,单价为76元,
故答案为76.
(2)①当0≤x≤10时,y=80x,
②∵单价不得低于50元,
∴降价了30元,购买了25件,
∴10<x≤25时,y=[80-2(x-10)]x=-2x2+100x,
③当x>25时,y=50x,
综上所述y=$\left\{\begin{array}{l}{80x}&{(0≤x≤10)}\\{-2{x}^{2}+100x}&{(10<x≤25)}\\{50x}&{(x>25)}\end{array}\right.$.
(3)①-2x2+100x=1050,解得x=15或35,
∵10<x≤25,
∴x=15.
②50x=1050,解得x=21,
21<25不合题意舍弃,
答:小明购买了15件这种服装.
点评 本题考查二次函数的应用、一元二次方程的应用、分段函数等知识,解题的关键是理解题意,正确求出分段函数的解析式,学会构建函数解决实际问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,秋千链子的长度OA=3m,静止时秋千踏板处于A位置.此时踏板距离地面0.3m,秋千向两边摆动.当踏板处于A′位置时,摆角最大,即∠AOA′=50°,则在A′位置,踏板与地面的距离为1.37m.(sin50°≈0.766,cos50°≈0.6428,结果精确到0.01m)
如图,秋千链子的长度OA=3m,静止时秋千踏板处于A位置.此时踏板距离地面0.3m,秋千向两边摆动.当踏板处于A′位置时,摆角最大,即∠AOA′=50°,则在A′位置,踏板与地面的距离为1.37m.(sin50°≈0.766,cos50°≈0.6428,结果精确到0.01m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
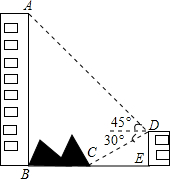 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com