
分析 首先移项,把等号右边的项移到等号左边,然后化成ax2+bx+c=0(a≠0).这种形式叫一元二次方程的一般形式.再根据其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项;c叫做常数项解答.
解答 解:x2+x+$\sqrt{3}$-3+2$\sqrt{3}$x=0,
x2+(1+2$\sqrt{3}$)x+$\sqrt{3}$-3=0,
方程${x^2}+x+\sqrt{3}=3-2\sqrt{3}x$化为标准形式是x2+(1+2$\sqrt{3}$)x+$\sqrt{3}$-3=0,其中a=1,b=1+2$\sqrt{3}$,c=$\sqrt{3}-3$.
故答案为:x2+(1+2$\sqrt{3}$)x+$\sqrt{3}$-3=0;1;1+2$\sqrt{3}$;$\sqrt{3}-$3.
点评 此题主要考查了一元二次方程的一般形式,关键是掌握一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
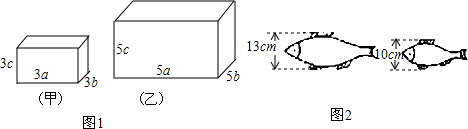
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x=\frac{{-2±\sqrt{5}}}{2}$ | B. | $x=\frac{{2±\sqrt{5}}}{2}$ | C. | $x=\frac{{1±\sqrt{5}}}{2}$ | D. | $x=\frac{{1±\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
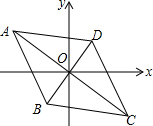 如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )| A. | a=-1,c=-$\sqrt{3}$ | B. | a=-2$\sqrt{3}$,c=-2 | C. | a=1,c=$\sqrt{3}$ | D. | a=2$\sqrt{3}$,c=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com