【答案】
分析:分两种情况进行讨论,①a=b,②a≠b,根据实数a、b满足a
2-8a+5=0,b
2-8b+5=0,即可看成a、b是方程x
2-8x+5=0的解,根据根与系数的关系列出关于a,b的等式即可求解.
解答:解:①当a=b时,原式=2;
②当a≠b时,
根据实数a、b满足a
2-8a+5=0,b
2-8b+5=0,即可看成a、b是方程x
2-8x+5=0的解,
∴a+b=8,ab=5.
则
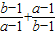
=
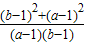
=
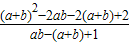
,
把a+b=8,ab=5代入得:
=
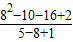
=-20.
综上可得
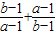
的值为2或-20.
故选C.
点评:本题考查了根与系数的关系,难度适中,关键是把a、b是方程x
2-8x+5=0的解,然后根据根与系数的关系解题.

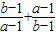 的值是( )
的值是( )
 名校课堂系列答案
名校课堂系列答案