
【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90°,得Rt△BDO,点B坐标为(0,﹣3),点C坐标为(0, ![]() ),抛物线y=﹣
),抛物线y=﹣ ![]() x2+bx+c经过点A和点C.
x2+bx+c经过点A和点C.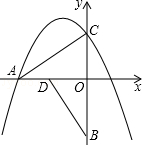
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?
【答案】
(1)
解:由旋转知:OA=OB=3.
∴A(﹣3,0).
由 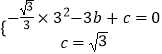 ,
,
∴ 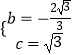 ;
;
(2)
解:存在,有2个Q点,坐标分别为:(﹣1, ![]() );(﹣1,
);(﹣1, ![]() ).
).
解答如下:设Q(﹣1,t).
∵A(﹣3,0),C(0, ![]() ),
),
∴AC= ![]() =2
=2 ![]() .
.
①当AC=AQ时,2 ![]() =
= ![]() ,
,
解得t=2 ![]() ,即Q(﹣1,
,即Q(﹣1, ![]() );
);
②当AC=CQ时,2 ![]() =
= ![]() ,
,
解得t= ![]() ,即Q(﹣1,
,即Q(﹣1, ![]() ).
).
(3)
解:∵OC= ![]() ,当 M、P、O、C为顶点得四边形是平行四边形时,PM=
,当 M、P、O、C为顶点得四边形是平行四边形时,PM= ![]()
∴M点的纵坐标为 ![]() 或﹣
或﹣ ![]() .
.
由 ![]()
解之,x=﹣2或0
由 ![]() ,
,
解之,x=﹣1+ ![]() 或﹣1﹣
或﹣1﹣ ![]() .
.
结合条件及图形分析得:OP=2或 ![]() +1,
+1,
∴当t=2或 ![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形.
+1秒时,以M、P、O、C为顶点得四边形是平行四边形.
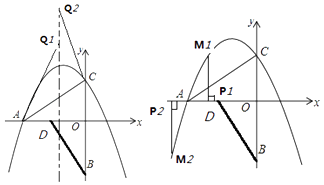
【解析】(1)由旋转的性质得OA=OB=3,从而得到点A的坐标,把点A、C的坐标分别代入函数解析式,然后利用待定系数法求b,c的值;(2)根据题意作出图形,结合图形易得点Q的坐标;(3)根据平行四边形的对边相等的性质和坐标与图形的性质进行解答.


科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
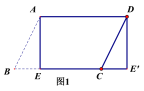
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
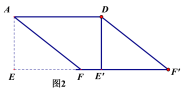
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):

(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两名运动员,选择一人参加市射击比赛,在选拔赛上,每人打10发,其中甲的射击成绩分别为10、8、7、9、8、10、10、9、10、9
①计算甲的射击成绩的方差;
②经过计算,乙射击的平均成绩是9,方差为1.4,你认为选谁去参加市射击比赛合适,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com