
分析 (1)根据3000吨以内,用水每吨收费0.5元,超计划部分每吨按0.8元收费,即可求解;
(2)根据收费标准,分x≤3000吨,和x>3000吨两种情况进行讨论,分两种情况写出解析式;
(3)该单位缴纳水费1540元一定是超过3000元,根据超过3000吨的情况的水费标准即可得到一个关于用水量的方程,即可求解.
解答 解:(1)某月该单位用水3200吨,水费是:3000×0.5+200×0.8=1660元;
若用水2800吨,水费是:2800×0.5=1400元,
故答案为:1400;1660;
(2)根据题意,当≤x≤3000时,y=0.5x;
当x>3000时,y=0.5×3000+0.8×(x-3000)=0.8x-900,
所以y关于x的函数解析式为:$\left\{\begin{array}{l}{y=0.5x(0≤x≤3000)}\\{y=-0.8x-900(x>3000)}\end{array}\right.$,
(3)因为缴纳水费1540元,所以用水量应超过3000吨,故令,设用水x吨.
1500+0.8(x-3000)=1540
x=3050
即该月的用水量是3050吨.
点评 本题考查的是用一次函数解决实际问题,正确理解收费标准,列出函数解析式是关键,此类题是近年中考中的热点问题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
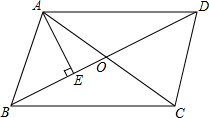 如图,平行四边形ABCD中,AC与BD相交于点O,∠ABD=2∠DBC,AE⊥BD.
如图,平行四边形ABCD中,AC与BD相交于点O,∠ABD=2∠DBC,AE⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 一 | 二 | 三 | 四 | 五 | 方差 | 日平均最高气温 |
| 最高气温 | 1℃ |  | -2℃ | 0℃ | 4℃ |  | 1℃ |
| A. | 2,2 | B. | 2,4 | C. | 4,2 | D. | 4,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{e}+\frac{2}{e}=\frac{3}{e}$ | B. | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}=\frac{x}{y}$ | ||
| C. | $\frac{a•b}{b•a}$=1 | D. | $\frac{0.2a+b}{0.7a-b}$=$\frac{2a+b}{7a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2b}{3}$ | B. | $\frac{\sqrt{2}}{2}b$ | C. | $\frac{\sqrt{3}}{2}b$ | D. | $\frac{\sqrt{3}}{3}b$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | $\sqrt{3}$+2 | C. | 1 | D. | -$\sqrt{3}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com