
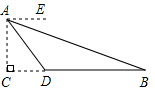
 为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27) 分析 根据AE∥BC知∠ADC=∠EAD=45°,根据AC⊥CD可得CD=AC=50,由∠ABC=∠EAB=15°,根据BC=$\frac{AC}{tan∠B}$求得BC的长即可求得BD的长.
解答 解:∵AE∥BC,
∴∠ADC=∠EAD=45°,
又∵AC⊥CD,
∴CD=AC=20米,
∵AE∥BC,
∴∠B=∠EAB=15°,
∴BC=$\frac{AC}{tan∠B}$=$\frac{20}{tan15°}$≈74.07(米),
∴BD=BC-CD=74.07-20≈54(米),
答:池塘B,D两地之间的距离约为54米.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并求解.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
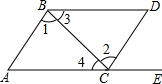 如图,点E在AC的延长线上,对于下列给出的四个条件:
如图,点E在AC的延长线上,对于下列给出的四个条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
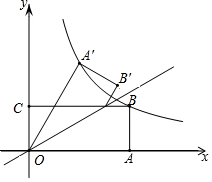 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com