
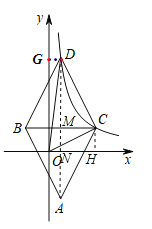
【题目】如图,在平面直角坐标系中,菱形ABDC的顶点D,C在反比例函数y=![]() 上(k>0,x>0),横坐标分别为
上(k>0,x>0),横坐标分别为![]() 和2,对角线BC∥x轴,菱形ABDC的面积为9.
和2,对角线BC∥x轴,菱形ABDC的面积为9.
(1)求k的值及直线CD的解析式;
(2)连接OD,OC,求△OCD的面积.

【答案】(1)k=2,y=﹣2x+5;(2)![]() .
.
【解析】
(1)连接AD,与BC交于点M,由点D,C横坐标分别为![]() 和2,得到CM=
和2,得到CM=![]() ,根据菱形的面积得到DM=3,设C(2,m),则D(
,根据菱形的面积得到DM=3,设C(2,m),则D(![]() ,m+3),列方程得到k=2,求得D(
,m+3),列方程得到k=2,求得D(![]() ,4),设直线CD的解析式为:y=kx+b,解方程即可得到结论;
,4),设直线CD的解析式为:y=kx+b,解方程即可得到结论;
(2)设AD与x轴交于N,过C作CH⊥x轴于H,根据S△COD=S四边形DNHC于是得到结论.
解:(1)连接AD,与BC交于点M,
∵菱形对角线BC∥x轴,
∴AD⊥BC,
∵点D,C横坐标分别为![]() 和2,
和2,
∴CM=![]() ,
,
∵菱形ABCD的面积为9,
∴2DMCM=9,
∴DM=3,
设C(2,m),则D(![]() ,m+3),
,m+3),
∵D,C在反比例函数y=![]() 的图象上,
的图象上,
∴2m=![]() (m+3),
(m+3),
∴m=1,
∴C(2,1),
∴k=2,
∴D(![]() ,4),
,4),
设直线CD的解析式为:y=kx+b,
∴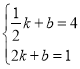 ,
,
解得:![]() ,
,
∴直线CD的解析式为y=﹣2x+5;
(2)设AD与x轴交于N,过C作CH⊥x轴于H.
∵S△NOD=S△COH=![]() ×2=1,
×2=1,
∴S△COD=S四边形DNHC=![]() (1+4)×
(1+4)×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=6,cosC=![]() ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
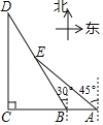
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
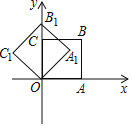
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
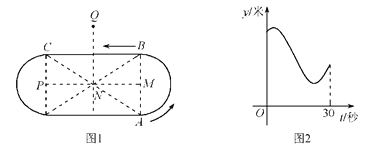
A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A. 4,3B. 6,3C. 3,4D. 6,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=![]() 的图象上,OA=5,OC=1,则△ODE的面积为( )
的图象上,OA=5,OC=1,则△ODE的面积为( )
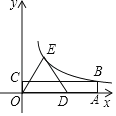
A.2.5B.5C.7.5D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com