
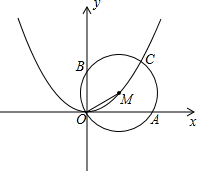
 如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.
如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$. 分析 作辅助线,构建正方形EOFC和全等三角形,证明△BEC≌△AFC,CE=CF,BE=AF,由A坐标和垂径定理得M的横坐标为1,代入抛物线得DM=a,由中位线定理得:OB=2a,设C(m,am2),根据CE=CF和AF=BE列方程组求出a的值.
解答  解:连接AB,AC,BC,
解:连接AB,AC,BC,
∵∠AOB=90°,
∴AB是⊙M的直径,
∴M在AB上,
∴∠ACB=90°,
∵$\widehat{CA}$=$\widehat{CB}$,
∴CA=CB,
过M作MD⊥x轴于D,
∴OD=AD=$\frac{1}{2}$OA=1,
∴M的横坐标为1,
当x=1时,y=a,
∴DM=a,
∵AM=BM,OD=DA,
∴DM是△AOB的中位线,
∴OB=2DM=2a,
过C作CE⊥y轴于E,过C作CF⊥x轴于F,
∴∠AOB=∠OEC=∠OFC=90°,
∴四边形EOFC是矩形,
∴∠ECF=90°,
∴∠ECB=∠FCA,
∵∠BEC=∠AFC=90°,
∴△BEC≌△AFC,
∴CE=CF,BE=AF,
∴矩形EOFC是正方形,
∴OF=OE=CF=CE,
设C(m,am2),
$\left\{\begin{array}{l}{m=a{m}^{2}}\\{2-m=m-2a}\end{array}\right.$,
解得:a=$\frac{-1±\sqrt{5}}{2}$,
∵a>0,
∴a=$\frac{-1+\sqrt{5}}{2}$,
故答案为:$\frac{-1+\sqrt{5}}{2}$.
点评 本题考查了正方形的性质、三角形中位线定理、垂径定理、圆中弧、弦的关系、抛物线上点的特征、三角形全等的性质和判定,明确在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.本题的关键是辅助线的作法.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
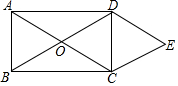 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
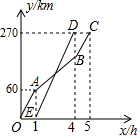 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
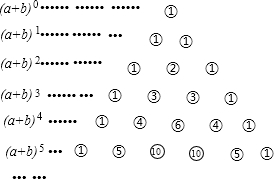
| A. | 2017 | B. | 2016 | C. | 191 | D. | 190 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com