
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
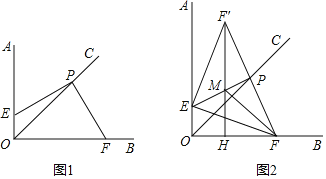
(1)如图1,求证:PE=PF;
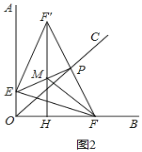
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
【答案】(1)见解析;(2)4.
【解析】
(1)过P作PG⊥OB于G,PH⊥AO于H,判定△PEH≌△PFG(AAS),即可得出PE=PF;
(2)依据轴对称的性质以及等腰直角三角形的性质,即可得到与∠EFM相等的角.
解:(1)如图1,过P作PG⊥OB于G,PH⊥AO于H,则∠PGF=∠PHE=90°,
∵OC平分∠AOB,PG⊥OB,PH⊥AO,
∴PH=PG,
∵∠AOB=∠EPF=90°,
∴∠PFG+∠PEO=180°,
又∵∠PEH+∠PEO=180°,
∴∠PEH=∠PFG,
∴△PEH≌△PFG(AAS),
∴PE=PF;
(2)由轴对称可得,∠EFM=∠EF′M,
∵F′H⊥OF,AO⊥OB,
∴AO∥F′F,
∴∠EF′M=∠AEF′,
∵∠AEF′+∠OEF=∠OFE+∠OEF=90°,
∴∠AEF′=∠OFE,
由题可得,P是FF′的中点,EF=EF′,
∴EP平分∠FEF′,
∵PE=PF,∠EPF=90°,
∴∠PEF=45°=∠PEF′,
又∵∠AOP=![]() ∠AOB=45°,且∠AEP=∠AOP+∠OPE,
∠AOB=45°,且∠AEP=∠AOP+∠OPE,
∴∠AEF′+45°=45°+∠OPE,
∴∠AEF′=∠OPE,
∴与∠EFM相等的角有4个:∠EF′M,∠AEF′,∠EFO,∠EPO.
故答案为:4.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
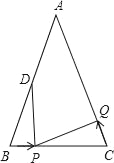
【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
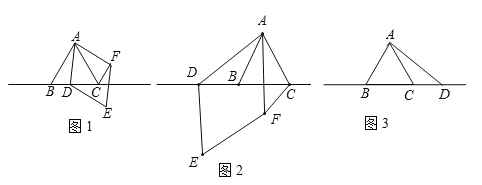
【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=![]() AB,求AG的长.
AB,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算):
价目表 | |
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元 |
请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5![]() ,则应交水费 元;3月份用水8
,则应交水费 元;3月份用水8![]() ,则应收水费 元;
,则应收水费 元;
(2)若该户居民4月份用水![]()
![]() (其中
(其中![]() ),则应交水费多少元(用含
),则应交水费多少元(用含![]() 的代数式表示,并化简);
的代数式表示,并化简);
(3)若该户居民5、6两个月共用水14![]() (6月份用水量超过了5月份),设5月份用水
(6月份用水量超过了5月份),设5月份用水![]()
![]() ,直接写出该户居民5、6两个月共交水费多少元(用含
,直接写出该户居民5、6两个月共交水费多少元(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出![]() 、
、![]() 、
、![]() 的值.
的值.![]() ,
,![]() ,
,![]() .
.
(2)![]() 、
、![]() 、
、![]() 所对应的点分别为
所对应的点分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 为一动点,其对应的数为
为一动点,其对应的数为![]() ,点
,点![]() 在
在![]() 、
、![]() 之间运动时,请化简式子:
之间运动时,请化简式子:![]() (请写出化简过程)
(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设经过
个单位长度的速度向右运动,假设经过![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .请问:
.请问:![]() 的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
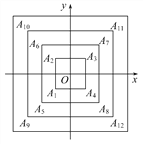
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com