
【题目】已知图中的曲线是反比例函数![]() 为常数)图象的一支.
为常数)图象的一支.
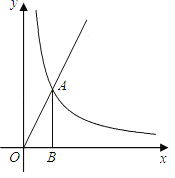
(1)这个反比例函数图象的另一支在第几象限?常数![]() 的取值范围是什么?
的取值范围是什么?
(2)若该函数的图象与正比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() ,过
,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,当
,当![]() 的面积为4时,求点
的面积为4时,求点![]() 的坐标及反比例函数的关系式.
的坐标及反比例函数的关系式.
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
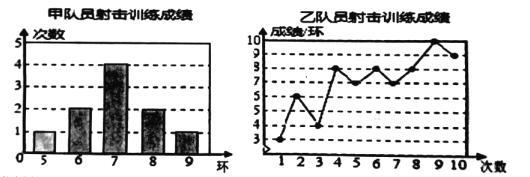
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
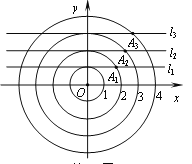
【题目】如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;……按照这样的规律进行下去,点An的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△AB1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去……,若点A(![]() ,0),B(0,2).则点B2019的坐标是( )
,0),B(0,2).则点B2019的坐标是( )
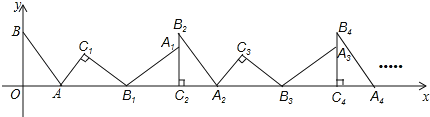
A.(6052,0)B.(6054,2)C.(6058,0)D.(6060,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.
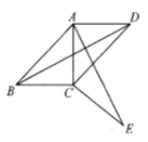
(1)请求出旋转角的度数;
(2)请判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
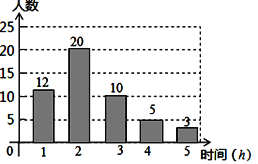
【题目】珠海市某中学在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
(1)被抽查学生阅读时间的中位数为 h,平均数为 h;
(2)若该校共有1500名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
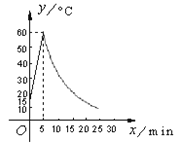
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com