
分析 结合整式加减法的运算法则进行求解即可.
解答 解:(1)原式=3.5-1.4-2.5-4.6
=-5.
(2)原式=[2-5×$\frac{1}{4}$]×(-4)
=$\frac{3}{4}$×(-4)
=-3.
(3)原式=[$\frac{5}{2}$-(-$\frac{5}{24}$)×24]÷5×(-1)
=$\frac{15}{2}$÷5×(-1)
=-$\frac{3}{2}$.
(4)原式=-4+3-8×$\frac{1}{3}$
=-1-$\frac{8}{3}$
=-$\frac{11}{3}$.
(5)原式=xy2-x2y-2 xy-2xy2+3x2y
=-xy2+2x2y-2xy.
(6)原式=5a2-[a2+5a2-2a-2a2+6a]
=5a2-[4a2+4a]
=a2-4a.
点评 本题考查了整式的加减,解答本题的关键在于熟练掌握整式加减法的运算法则.


科目:初中数学 来源: 题型:选择题
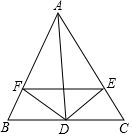 如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,点A(0,6),点B(-8,0),过A点的直线交x轴于点C,当△ABC是以AB为底的等腰三角形时,直线AC对应的函数关系式为y=$\frac{24}{7}$x+6.
如图,在平面直角坐标系xOy中,点A(0,6),点B(-8,0),过A点的直线交x轴于点C,当△ABC是以AB为底的等腰三角形时,直线AC对应的函数关系式为y=$\frac{24}{7}$x+6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么$\frac{BD}{AB}$的值是$\frac{\sqrt{5}-1}{2}$.
如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么$\frac{BD}{AB}$的值是$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com