
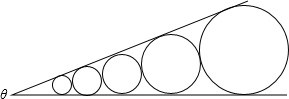
如图,半径不等的⊙O1,⊙O2外离,线段O1O2分别交⊙O1,⊙O2于点A,B,MN为两圆的公切线,分别切⊙O1,⊙O2于点M,N,连接MA,NB.请判断∠AMN与∠BNM的大小关系,并证明你的结论.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.
如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.| BP |
| PM |
| NQ |
| QB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.
如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.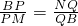 ;②△KPM∽△NQK.
;②△KPM∽△NQK.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com