
【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.在下列解答中,填空:
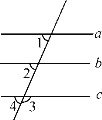
(1)因为∠1=68°,∠2=68°(已知),
所以__________(等量代换).
所以____∥_____________________________.
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°
,所以____________
又因为∠2=68°,
所以___________(等量代换),
所以____∥_________________________________.
【答案】 ∠1=∠2 a b 同位角相等,两直线平行 ∠4=68° ∠2=∠4 b c 同位角相等,两直线平行
【解析】
(1)因为∠1和∠2是直线a和直线b被第三条直线所截的同位角,且∠1=68°,
∠2=68°,根据同位角相等,两直线平行可得:a//b,
(2)因为∠4和∠3是邻补角,所以∠4=180°-∠3,即∠4=68°, 因为∠2和∠4是直线b和直线c被第三条直线所截的同位角,且∠2=∠4,根据同位角相等,两直线平行可得: b//c.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2 (等量代换).
所以a//b, 同位角相等,两直线平行,
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°,
又因为∠2=68°,
所以∠2=∠4 (等量代换),
所以b//c同位角相等,两直线平行.
故答案为:∠1=∠2, a ,b , 同位角相等,两直线平行, ∠4=68°, ∠2=∠4 ,b ,c ,
同位角相等,两直线平行.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
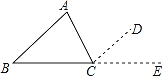
【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 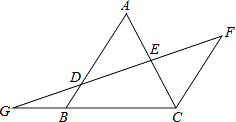
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 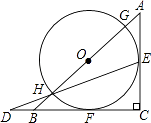
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com