
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
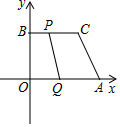 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 悉尼 | 纽约 |
| 时差/时 | +2 | -13 |
| A. | 6月16日1时;6月15日10时 | B. | 6月16日1时;6月14日10时 | ||
| C. | 6月15日21时;6月15日10时 | D. | 6月15日21时;6月16日12时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
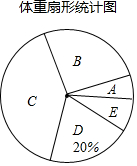 某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:| 组边 | 体重(千克) | 人数 |
| A | 45≤x<50 | 12 |
| B | 50≤x<55 | m |
| C | 55≤x<60 | 80 |
| D | 60≤x<65 | 40 |
| E | 65≤x<70 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com