练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．求下列各式中x的值
    27×9x=3x+1．

    分析 先将27×9x变形为33×32x，然后结合幂的乘方与积的乘方的运算法则得出3+2x=x+1，求出x值即可．

    解答 解：∵27×9x=3x+1，
    ∴33×32x=3x+1，
    ∴3+2x=x+1，
    解得：x=-2．

    点评 本题考查了幂的乘方与积的乘方，解答本题的关键在于先将27×9x变形为33×32x，然后结合幂的乘方与积的乘方的运算法则得出3+2x=x+1，再求出x值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．某商场元旦促销，将某种书包每个x元，第一次降价打“八折”，第二次降价每个又减18元，经两次降价后售价为102元，则所列方程是（　　）
    A．x-0.8x-18=102B．0.08x-18=102C．102-0.8x=18D．0.8x-18=102

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列各式计算正确的是（　　）
    A．$\sqrt{9}$=±3B．4$\sqrt{3}$-3$\sqrt{3}$=1C．（$\sqrt{2}$）2=4D．$\sqrt{27}$÷$\sqrt{3}$=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．若两个实数的积是-1．则称这两个实数互为负倒数，如2与-$\frac{1}{2}$互为负倒数，
    （1）判断（4+$\sqrt{2}$）与（4-$\sqrt{2}$）是否互为负倒数，并说明理由；
    （2）若实数（$\sqrt{x}$+$\sqrt{y}$）是（$\sqrt{x}$-$\sqrt{y}$）的负倒数，求点（x，y）中纵坐标随横坐标变化的函数解析式，并画出函数图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

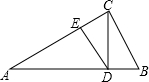
    1．将一副直角三角尺BAC和ADE如图放置，其中∠BCA=30°，∠AED=45°，若∠AFD=75°，试判断AE与BC的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（　　）
    A．$\frac{1}{2}$B．$\frac{2}{3}$C．$\frac{\sqrt{2}}{2}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．若（x2+y2-1）2=36，求x2+y2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在平面直角坐标系中，⊙P的半径为4，圆心P坐标是（4，a）（a＞4），函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$，则a的值是4+2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知：如图所示，直线MA∥NB，∠MAB与∠NBA的平分线交于点C，过点C作一条直线l与两条直线MA，NB分别相交于点D，E．

    （1）如图1所示，当直线l与直线MA垂直时，补全图形并猜想线段AD，BE，AB之间的数量关系（直接写出结论，不用证明）；
    （2）如图2所示，当直线l与直线MA不垂直且交点D，E都在AB的同侧时，补全图形并探究（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由；
    （3）当直线l与直线MA不垂直且交点D，E在AB的异侧时，补全图形并探究（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD，BE，AB之间还存在某种数量关系吗？如果存在，请直接写出它们之间的数量关系．

    查看答案和解析>>

    同步练习册答案