
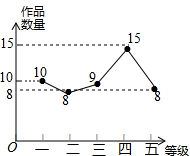
 ijУ���ú��ٽ��пƼ�ʵ�������ѧ֮���ˣ�1����Ը����Ͻ��ġ��Ƽ���Ʒ��������������ͳ�ƣ�����������ͼ������ͳ��ͼ��
ijУ���ú��ٽ��пƼ�ʵ�������ѧ֮���ˣ�1����Ը����Ͻ��ġ��Ƽ���Ʒ��������������ͳ�ƣ�����������ͼ������ͳ��ͼ������ ��1����������ͳ��ͼ�õ����ȼ�����Ʒ������Ȼ��ѵȼ��ļ�����Ӽ��ɣ�
��2������ƽ��������������λ���Ķ�����⣻
��3���Ȼ���״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ��鵽����Ʒǡ����A��B�Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
��� �⣺��1��10+8+9+15+8=50��
���ˣ�1����յ��ġ��Ƽ���Ʒ��50����
��2��ƽ����=$\frac{1}{5}$��50=10��������
����Ϊ�ĵȼ�����λ��Ϊ���ȼ���
��3������״ͼΪ��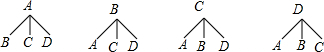
����12�ֵȿ��ܵĽ���������г鵽����Ʒǡ����A��B�Ľ����Ϊ2��
���Գ鵽����Ʒǡ����A��B�ĸ���=$\frac{2}{12}$=$\frac{1}{6}$��
���� ���⿼�����б�������״ͼ����ͨ���б�������״ͼ��չʾ���еȿ��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ����¼�A��B�ĸ��ʣ�Ҳ��������������λ����ͳ��ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
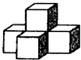 ��ͼ��һ����5����ͬ����������ɵ�����ͼ�Σ����ĸ���ͼ�ǣ�������
��ͼ��һ����5����ͬ����������ɵ�����ͼ�Σ����ĸ���ͼ�ǣ�������| A�� |  | B�� |  | C�� | 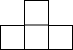 | D�� | 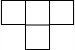 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������������y=$\frac{a}{x}$������������y=bx��ͬһ����ϵ�еĴ���ͼ������ǣ�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������������y=$\frac{a}{x}$������������y=bx��ͬһ����ϵ�еĴ���ͼ������ǣ�������| A�� | 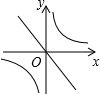 | B�� | 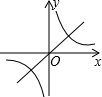 | C�� | 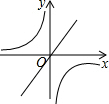 | D�� | 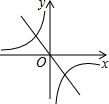 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ���������ȥһ�Ǻ�õ��ļ����壬��������ͼ�ǣ�������
��ͼ��һ���������ȥһ�Ǻ�õ��ļ����壬��������ͼ�ǣ�������| A�� |  | B�� |  | C�� | 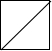 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
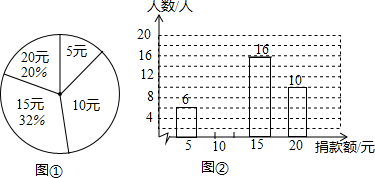
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
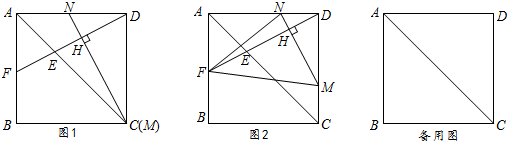
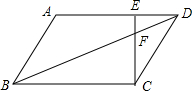 ��ͼ����ƽ���ı���ABCD�У���E�DZ�AD��һ�㣬��AE=2ED��EC���Խ���BD�ڵ�F����$\frac{EF}{FC}$���ڣ�������
��ͼ����ƽ���ı���ABCD�У���E�DZ�AD��һ�㣬��AE=2ED��EC���Խ���BD�ڵ�F����$\frac{EF}{FC}$���ڣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com