
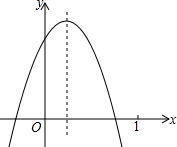
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①:首先根据对称轴为x=-$\frac{b}{2a}$>0,可得$-\frac{b}{a}$>0,所以方程ax2+bx+c=0的两根之和大于0,据此判断即可.
②:首先根据抛物线与y轴的交点在y轴的上方,可得c>0;然后根据当x=1时,y<0,可得a+b+c<0,所以a+b<0,据此判断即可.
③:根据在对称轴的右边,y随x的增大而减小,可得结论③不正确.
④:根据0<-$\frac{b}{2a}$<1,抛物线与x轴的一个交点0<x1<1,可得抛物线与x轴的另一个交点-1<x2<0,所以当x=-1时,y<0,据此判断即可.
⑤:首先根据抛物线开口向下,可得a<0,然后根据对称轴为x=-$\frac{b}{2a}$>0,可得b>0;最后根据对称轴为x=-$\frac{b}{2a}$<1,可得2a+b<0,再根据-2b<0,判断出2a-b<0即可.
解答 解:∵对称轴为x=-$\frac{b}{2a}$>0,
∴$-\frac{b}{a}$>0,
∴方程ax2+bx+c=0的两根之和大于0,
∴结论①正确.
∵抛物线与y轴的交点在y轴的上方,
∴c>0;
∵当x=1时,y<0,
∴a+b+c<0,
又∵c>0,
∴a+b<0,
∴结论②正确.
∵在对称轴的右边,y随x的增大而减小,
∴y随x的增大而增大不正确,
∴结论③不正确.
∵0<-$\frac{b}{2a}$<1,抛物线与x轴的一个交点0<x1<1,
∴抛物线与x轴的另一个交点-1<x2<0,
∴当x=-1时,y<0,
∴a-b+c<0,
∴结论④正确.
∵抛物线开口向下,
∴a<0,
∵对称轴为x=-$\frac{b}{2a}$>0,
∴b>0;
又∵对称轴为x=-$\frac{b}{2a}$<1,
∴2a+b<0,
又∵-2b<0,
∴2a-b<0,
∴结论⑤不正确.
综上,可得
正确的结论有3个:①②④.
故选:B.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:填空题
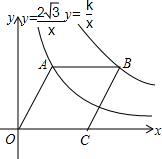 如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.
如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
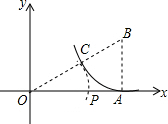 如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
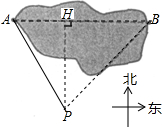 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
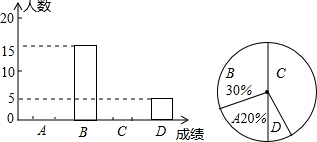 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:| 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
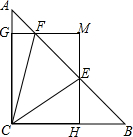 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
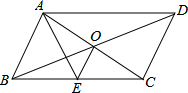 如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④OE=$\frac{1}{4}$BC,成立的个数有( )
如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④OE=$\frac{1}{4}$BC,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com