
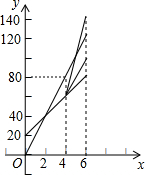
 某部队甲、乙现两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.
某部队甲、乙现两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.分析 (1)根据函数图象中的数据可以分别求得当0≤x≤4时,y甲、y乙与x之间的函数关系式;
(2)根据(1)中的函数解析式,将x=6代入求它们的和,然后与180比较,即可解答本题;
(3)根据题意,可以分两种情况,分别求出乙班增加人数后平均每小时植树的数量即可解答本题.
解答 解:(1)设y甲=k1x,
将坐标(4,80)代入,得
则4k1=80,
∴k1=20,
∴y甲=20x,
当x=2时,y乙=y甲=20×2=40,
设y乙=k2x+b2,
将(0,20)和(2,40)分别代入,
$\left\{\begin{array}{l}{{b}_{2}=20}\\{2{k}_{2}+{b}_{2}=40}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{k}_{2}=10}\\{{b}_{2}=20}\end{array}\right.$,
∴y乙=10x+20;
(2)当x=6时,
y甲+y乙=20×6+10×6+20=120+80=200>180,
即甲、乙两班植树的总量之和能超过180棵;
(3)甲班6小时的植树总量为:y甲=20×6=120(棵),
①若活动结束后乙班植树总量比甲班少20棵,
则y乙=120-20=100,
设y乙=k3x+b3,
将(4,60)和(6,100)分别代入,得
$\left\{\begin{array}{l}{4{k}_{3}+{b}_{3}=60}\\{6{k}_{3}+{b}_{3}=100}\end{array}\right.$,得$\left\{\begin{array}{l}{{k}_{3}=20}\\{{b}_{3}=-20}\end{array}\right.$,
∴y乙=20x-20(4≤x≤6),
即乙班增加人数后平均每小时植树20棵;
②若活动结束后甲班植树总量比乙班少20棵,
则y乙=120+20=140,
设y乙=k4x+b4,
将(4,60)和(6,140)分别代入,得
$\left\{\begin{array}{l}{4{k}_{4}+{b}_{4}=60}\\{6{k}_{4}+{b}_{4}=140}\end{array}\right.$,得$\left\{\begin{array}{l}{{k}_{4}=40}\\{{b}_{4}=-100}\end{array}\right.$,
∴y乙=40x-100(4≤x≤6),
即乙班增加人数后平均每小时植树40棵;
答:乙班增加人数后平均每小时植树20棵或40棵.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $m<\frac{5}{2}$ | B. | $m>\frac{5}{2}$ | C. | $m<\frac{5}{2}$且m≠2 | D. | $m>\frac{5}{2}$且m≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10100 | B. | 10200 | C. | 10300 | D. | 10400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com